本文转自头条号
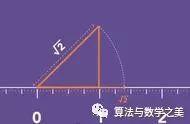
恭喜你,不经意间发现了史上的第一次数学危机。如果在2500年前,你也许会被当作异端扔进海里哦。这事还得从公元前580~568之间的古希腊说起。

当时数学家毕达哥拉斯(Pythagoras)建立了毕达哥拉斯学派。这一学派集宗教、科学和哲学于一体,他们认为万物皆数,即宇宙间的一切现象都能归结为整数或整数之比。但是该学派的成员希伯索斯(Hippasus)根据勾股定理(西方称为毕达哥拉斯定理)通过逻辑推理发现,边长为1的正方形的对角线长度既不是整数,也不是整数的比所能表示的。希伯索斯的发现被人们看成是荒谬和违反常识的事。它不仅严重触犯了毕氏学派的信条,同时也冲击了当时希腊人的传统见解,使古希腊的数学家们感到惊奇和不安,所以这一事件在数学史上称为第一次数学危机。希伯索斯的发现终没有被毕达哥拉斯学派的信徒们所接受,相传毕氏学派就因这一发现而把希伯索斯投入海中处死。

越来越多无理数的发现迫使希腊数学家不得不研究这些数。欧多克斯(Eudoxus,约公元前408~前347)首先引入了“量”的概念,这里的量不是数,而是代表诸如线段、角、面积、体积、时间等。量与数的不同在于,数是离散的,即可数的,而量可以是连续的。欧多克斯由量的概念出发给出了一种新的比例论。欧几里得《几何原本》第五卷中引用了这种比例论,其定义为:设A,B,C,D是任意四个量,其中A和B同类(即均为线段、角或面积等),C和D同类。如果对于任何两个正整数m和n,mA大于、等于、小于nB是否成立,相应地取决于mC大于、等于、小于nD是否成立,则称A与B之比等于C与D之比,即A,B,C,D四量成比例。通过这一新的比例论,希腊数学家可以严格地将可公度量的证明推广到不可公度的量,从而解决了不可公度带来的逻辑上的矛盾。
欧多克斯比例论实际上是为了避免把无理数当作数,这个理论给不可公度量的比例提供了逻辑依据,但是也将数同几何截然分开,而且使希腊数学的重点从数转向了几何,因为几何可以处理无理数。在此后的几千年间,几何学成为几乎是全部严密数学的基础,而算术和代数则没有取得独立的地位。
第一次数学危机的彻底解决,是在危机产生二千年后的19世纪,建立了极限理论和实数理论之后,才被彻底解决的。

