本文节选自论文 基于样本加权的格拉斯曼平均算法

传统 PCA 算法没有对样本进行加权处理，离群样本与其他样本对算法产生的影响是相同的。要通过为离群点赋予很小的权值，提高 PCA 的鲁棒性，降低异常值对算法运算精度的影响。采用高斯函数求出样本的权重矩阵W_n×n ，计算公式如下：

其中τ是一个超参数。D(i)被定义为在d维空间中数据点xi与其他数据点相似性的总和，而矩阵W为一对称矩阵，从而得到D(i)的计算公式如下：

其中D是一个n维向量，该向量的每一个成分都表示了数据点x_i的全局密度，而数据点的权重p(xi)则与对应点的密度成正比：

虽然等式（14）和（15）提供了一种权重策略，但是它考虑了数据的所有可能数据点。还需要考虑数据的内在特性，即数据的分布是不平均的。即使是同类数据，它们之间的分布也可能比较分散，甚至也有不同类数据分布比较接近的可能，即位于边界上的数据点。对于个xi数据点，搜索它的k个最近邻点，表示为y₁,y₂,⋯,y_k。当类别信息提供时，搜索同类内的k个最近邻点。

利用这些信息计算每个样本的局部权重，表示为：

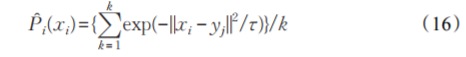
当类别信息没有提供时，并没有采用等式（15）去归化权重，直接利用了等式（16）。很显然P̂(xi)位于[0，1]区间。但是对于分类问题，由于类别信息是已知的，所以考虑在等式（16）的基础上继续归化权重，使得每类样本的权重之和等于1。因为在原算法中，式（8）中的权重如式（9）所示，即选取了数据的模，仅完成了数据的归一化，从而得到等式（11）的优化模型，很显然等式（11）没有对各数据的离群点进行判别和抑制，致使这种子空间的投影没有去除掉异常样本的影响。为了找到上述的格拉斯曼平均子空间，在权重的基础上，提出了下面的优化模型，表示为：

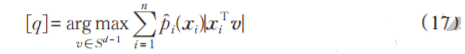
对于模型（17）提出了下面算法。

算法1：加权的格拉斯曼平均

（1）对于每个数据点，计算每个数据点的k最近邻点，利用等式（16）计算每个样本的权重。

（2）q(0)初始化为随机的d维列向量，令q(0)=q(0)/||q(0)||，并将迭代次数j初始化为1。

（3）任意样本xi带上权重p(xi)后取符号位∂i(j)=。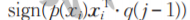

（4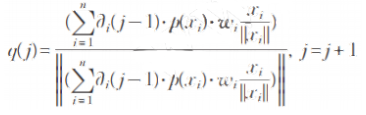），其中。

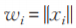（5）若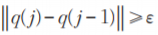且小于最大迭代次数M，执行第（3）步，否则，提取成分q(j)作为当前数据的第一主成分。

显然算法1仅仅取得了一个投影向量，除去计算权重时的复杂性，算法1的计算复杂性是O(ndM)，其中M是最大的迭代次数。同时，算法的尺度性较好。在实际情况下，往往利用xˉ_i=x_i-q^Tqx_i处理每个数据点来得到新的数据点，然后在新的数据点的基础上得到另外一个投影向量。当一个投影向量得到后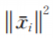，2可以2的大小，就可以找到样本集中包含的离群点。这样可以根据重建误差对每个数据点排序，去除重建误差比较大的数据点，进而尽可能地去除掉离群点。当然可以利用数据点的重建误差重新计算权重，从而提高计算权重的鲁棒性。表示第i个数据点的重建误差，根据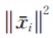的大小，就可以找到样本集中包含的离群点。这样可以根据重建误差对每个数据点排序，去除重建误差比较大的数据点，进而尽可能地去除掉离群点。当然可以利用数据点的重建误差重新计算权重，从而提高计算权重的鲁棒性。

论文原文：基于样本加权的格拉斯曼平均算法.pdf