转自公众号算法与数学之美

数学抽象性和空间性非常大，对孩子的逻辑思维和发散思维有较高的要求，很多因素可能导致孩子们对数学产生了畏惧的心理，认为数学不管怎么学都没有提升了，导致很多同学干脆放弃了。

为了让孩子喜欢上数学，今天与各位一同分享几则神奇的数学动图，非常形象生动，很多难以理解的数学定理，简直看完一目了然。希望能帮孩子们找到学习的动力，并让他们爱上数学！

1、被简单证明的勾股定理

给三角形加上一点厚度。从面积问题，跳转到了具象的体积问题。

2、勾股定理的面积证明法

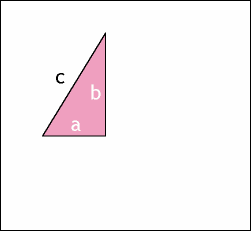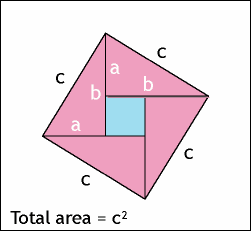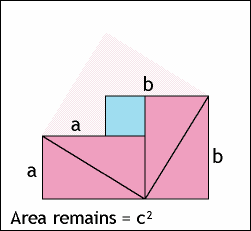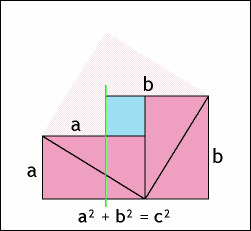
It's a long story……慢慢看。

3、周长和直径的π点小事

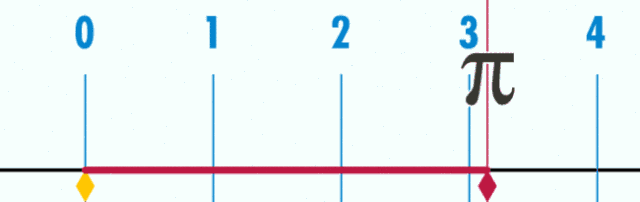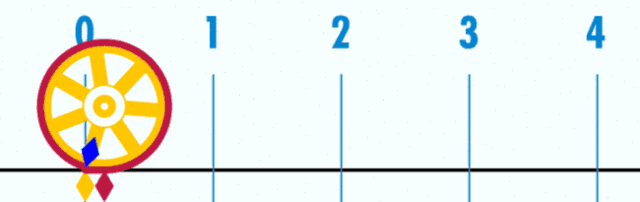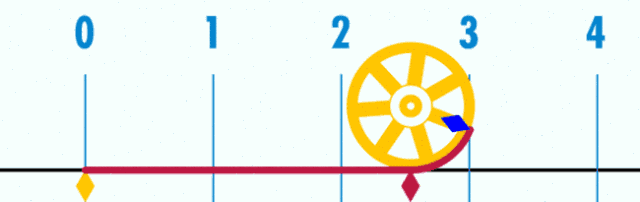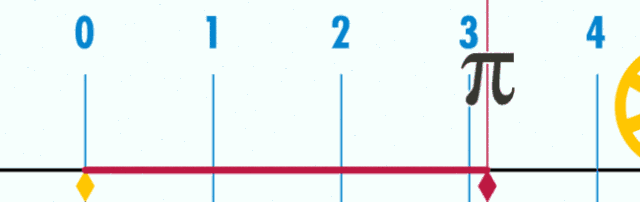
4、圆的面积=2πr?

首先，把圆解剖为一个三角形。底边是周长。然后根据三角形的面积推出圆的面积，so easy~

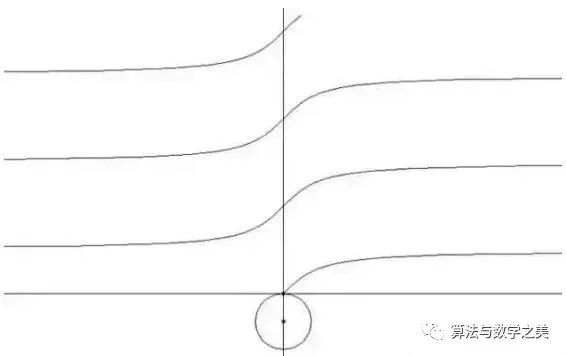
5、正切值曲线

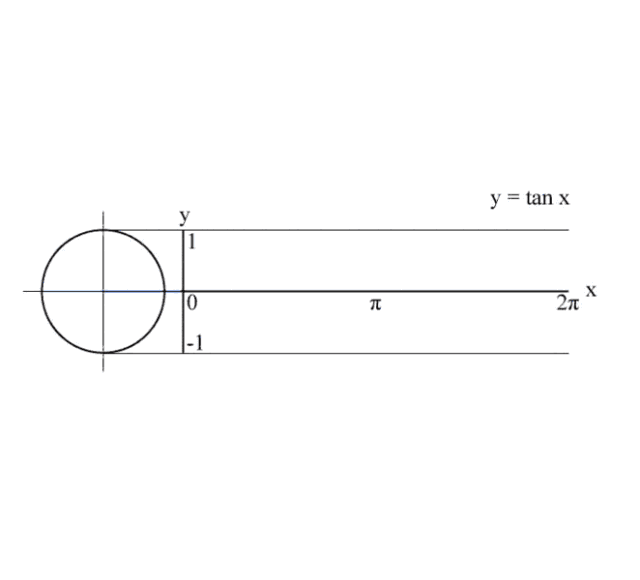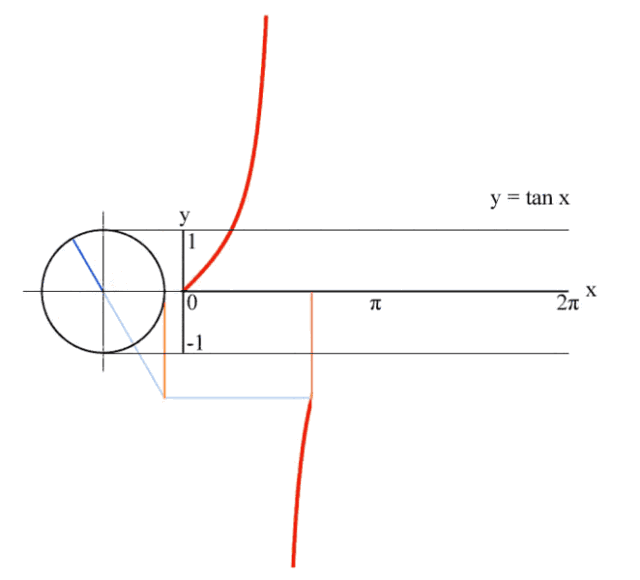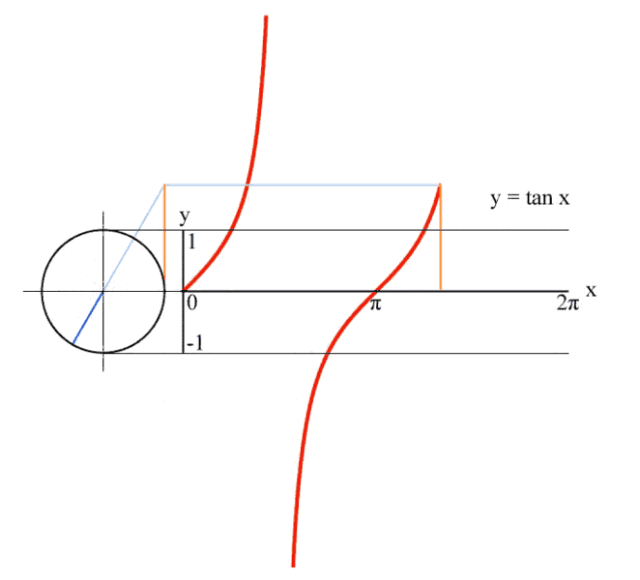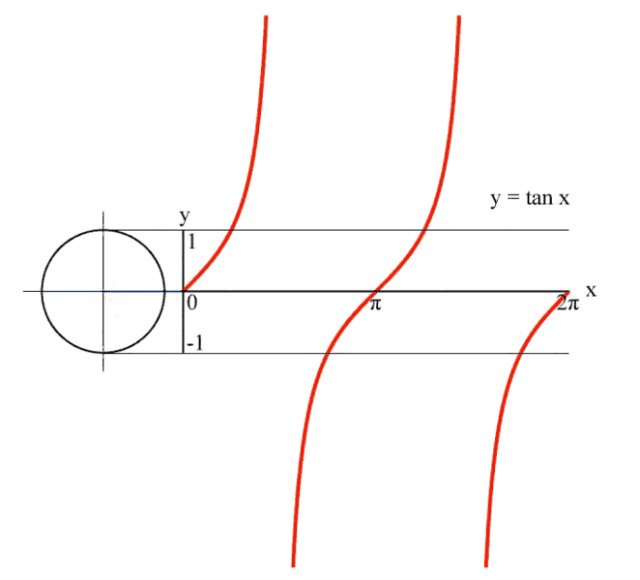
这是一个正切线被θ牢牢控制，一辈子都逃不出其手掌心的故事。

6、看懂上面那个，就不解释这个了

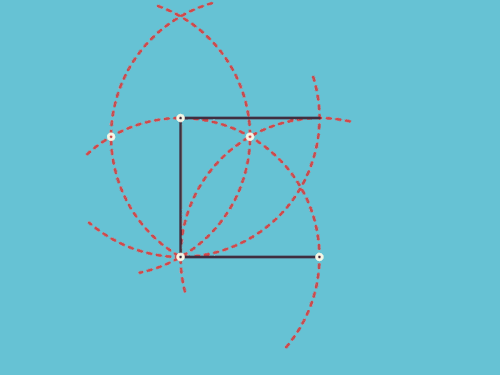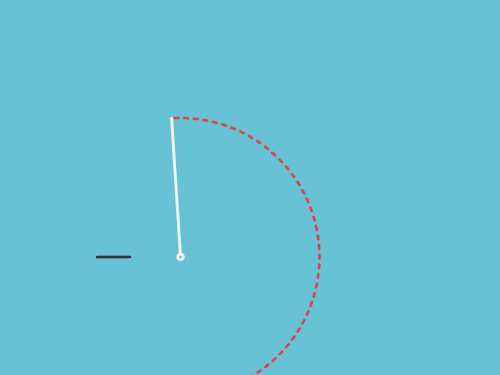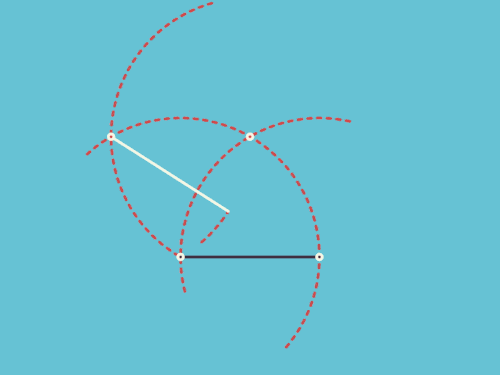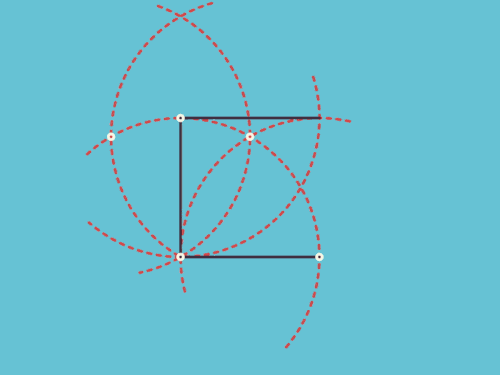
7、圆规和正方形的爱恨纠缠

8、认识椭圆的第一天，每个老师都会做的事

两个绿点，代表了坐在第一排，强制被叫上讲台按线头的两位同学。

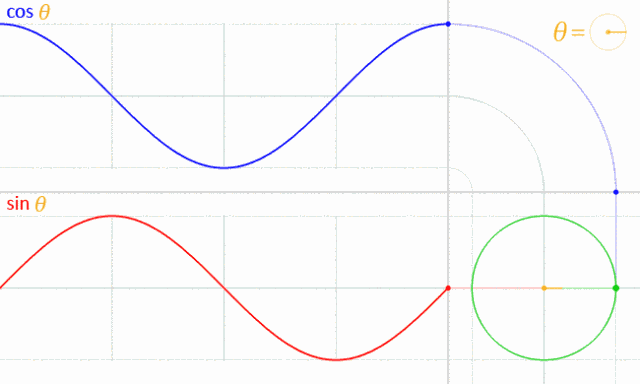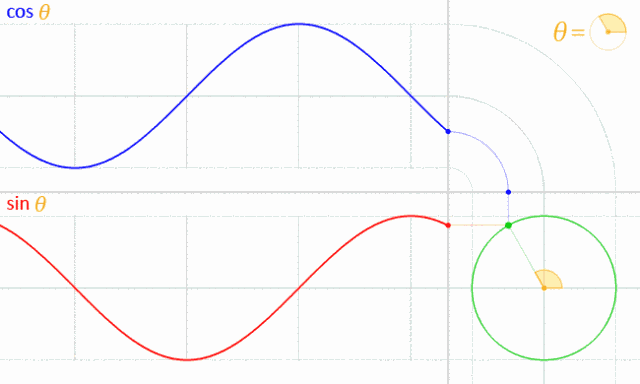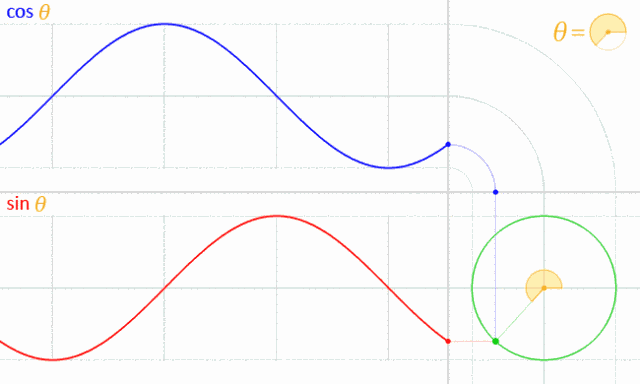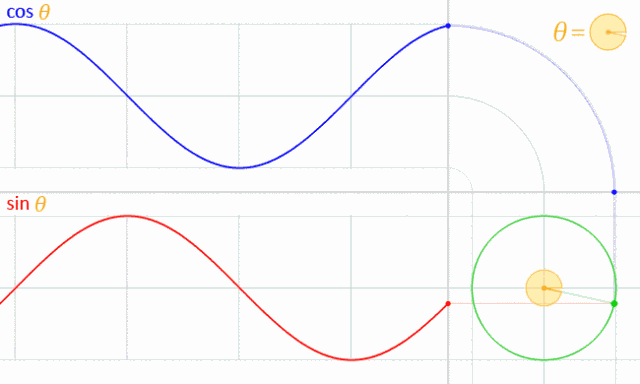
9、考赛因和赛因的你追我赶

10、谢尔宾斯基三角形

这是一种分形，在等边三角形里挖掉等边三角形再挖掉等边三角形再挖掉等边三角形……最后它得以永生。

11、得到永生的证明

12、最后，放一张数学家很会玩之胖子超人的诞生

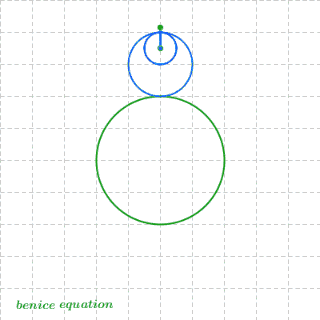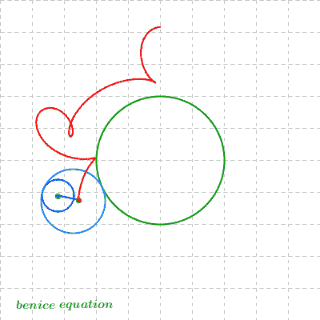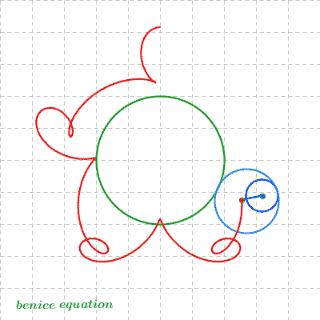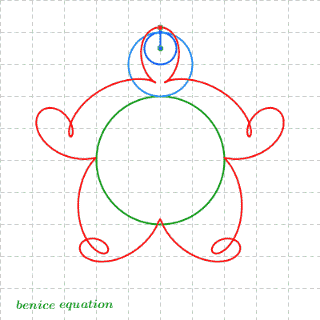
13、三角函数

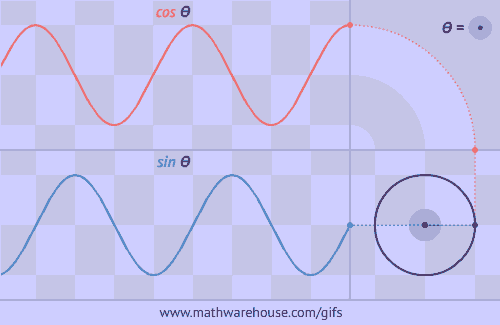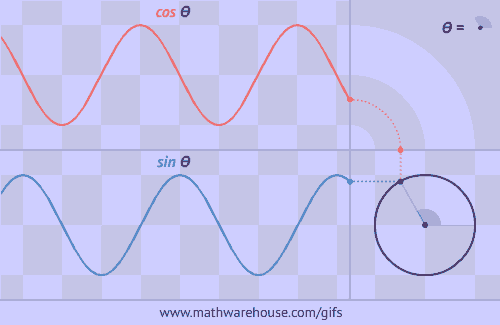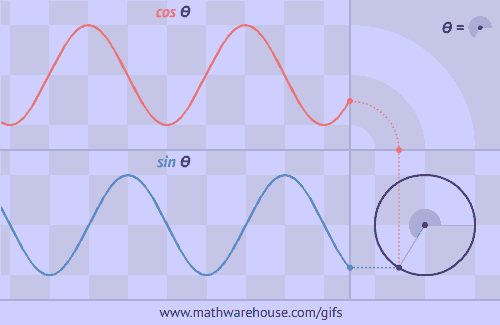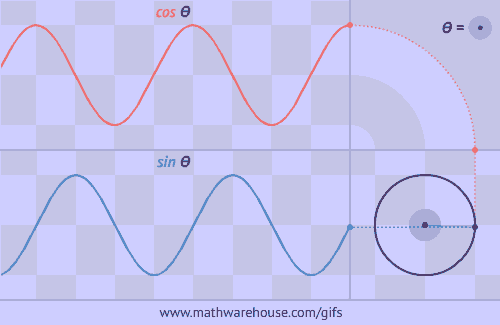
正弦函数和余弦函数的波浪形是怎么回事呢？原来可以看成一点在圆上运动在坐标轴上的投影啊！

14、杨辉三角

它首次出现在南宋杨辉的《详解九章算术》，因此得名。它的前几层是这样的：

每一层中的数字，等于它上边两个数的和。那么这些数字有什么用呢？其实这里边的数字是括号平方（或立方、四次方等）的展开系数：

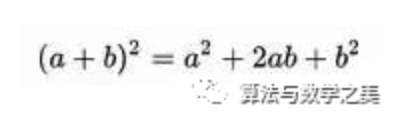
等号右边的2 就对应于杨辉三角第三层中的2。如果是三次方展开括号，就用第4 层中的数字，以此类推。

15、计算1+2+3……

怎么计算1+2+3……+100？如果直接算就太麻烦啦！但是我们换一个方法：

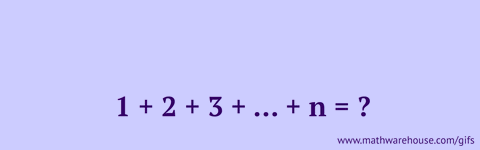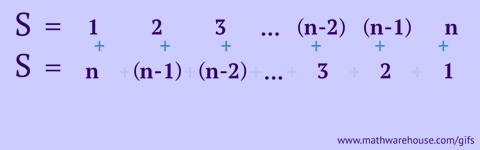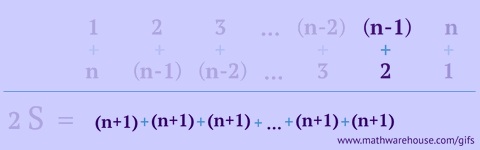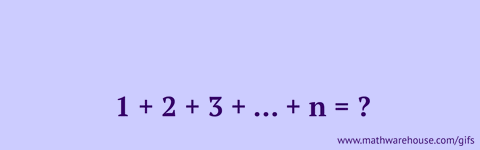
把第二列调换顺序，1+2+3……+100 就可以变成50 个 （1+100），也就是5050。你也可以用其他数字试一试，是不是很神奇？