本文转自 清华小五爷园

最近几天，数学界可谓是出现了一次“大地震”。就在9月24日，数学家迈克尔·阿提亚( Michael Atiyah)爵士在海德堡举办的一次论坛上，向全世界展示了他证明黎曼猜想(Riemann Hypothesis)的全过程。 

根据一份谷歌云盘中的预印本显示，阿提亚爵士的证明仅有5页纸。鉴于这篇文章尚未通过同行评议，一些学者对此次证明仍存在质疑；但无论如何，本次证明使得这个1859年提出的古老猜想再次引发了数学界和吃瓜群众界的热烈讨论。 

阿提亚爵士最新证明的引言部分 

而作为一名吃瓜群众，如何在大佬/巨佬们谈笑风生的时候，不至于只能在一旁尴尬地微笑？小编将用接下来的时间为大家科普黎曼猜想的前世今生，相信看完本文，各位吃瓜群众应该会对黎曼猜想有一个全新的认识。 

第10000个素数是多少？ 

要了解黎曼猜想，就必须先了解素数。素数是除了1和它本身外没有其他因子的大于1的整数。那么根据这个定义，只要给我们足够多的时间，我们总可以判断一个数是否是素数，最原始的办法就是用比他小的数2，3，4……去除这个数，一直到这个数平方根为止，如果都不能除尽，那么这个数就是素数。 

根据唯一分解定理，任意一个大于1的整数都可以唯一地写成一些素数的乘积（不分次序），那么我们可以把素数看作是砖石，或单个或互相组合构成了大大小小的整数，与1一块填上了无限长的数轴正半轴上每一个代表整数的坑。 

素数就好像是化学里的基本元素，但素数远比周期表上排的整整齐齐的元素要麻烦，因为它们之间似乎并无规律可循，而且素数的数量要多得多。 

素数数量众多且无规律性 

素数最常见的一个性质就是素数的无穷性，换言之，就是任意选一个数，都有一个比它大的素数。 

用反证法很容易证明：如果素数有限，就把他们都乘起来再加个1，那么这有限个素数都不是这个新数的因子，这就产生了矛盾。当然，这一条性质连冰山一角都算不上，远远不能满足我们的求知欲。 

从欧几里得用上述方法证明无穷性后很多年过去了，我们获得了一些非常漂亮的成果，比如Chebyshev定理（对于充分大的n，n与2n之间必有素数），Dirichlet定理（在相邻两项互素的等差数列中有无穷多项为素数）等等。但我们还是希望，能有一个简单的方便计算的函数形式，清楚地告诉我们第几个素数是多少。 

欧几里得 

很遗憾，两千多年过去了，这样的函数并没有被给出。但人们通过对前若干素数的列举，发现素数的分布还是有一定的规律，至少在整体数量上是如此。如果我们记π(x)为不大于x的素数个数，那么我们从下表可以看到，π(x)基本上与x/ln x是很接近的。 

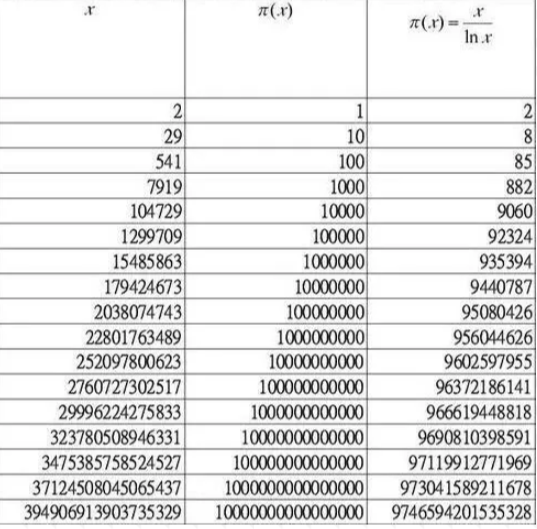
素数分布与x/ln x 

这个估计，最早是Gauss和Legendre提出的，并在快100年后被Hadamard等人证明，现在被称作素数定理。他们的证明，用到了Gauss学生Riemann的《论小于给定值的素数的个数》中的一些重要结论和思路。 

Riemann的论文 

1826年，Riemann（黎曼）生于德国的一个小镇。他的父亲是一名牧师，家中一共有六个孩子，他排行第二。他的同事Dedekind是少数几个能和他说上话的人，据他回忆，Riemann是个安静害羞的人，且长期身体不佳，喜欢独处。 

Dedekind 

1846年，Riemann顺利进入哥廷根大学学习哲学和神学，期间去听了很多数学讲座，从此矢志于此。他的父亲本来只希望他能顺利毕业继承牧师的事业，但后来还是很支持Riemann决定选择他自己更感兴趣的数学。 

在十九世纪三四十年代，哥廷根大学是一个死气沉沉的地方，只有Gauss带来的一丝生机。当时世界的数学中心是巴黎和柏林，前者有Cauchy和Fourier，他们全面建设了分析学，后者则有算术学的Dirichlet，代数学的Jacobi，几何领域的Steiner，以及分析学的Eisenstein等的全面突破。 

哥廷根大学 

于是在Riemann 20岁的那年春天，对哥廷根略感失望的他来到了柏林，在这里，他遇到了给他最心仪的“严肃数学”研究指明道路的Dirichlet等大师。几年后他顺利地获得博士学位，并在论文中开创了函数的几何理论，提出了著名的复变函数可导的充分必要条件——柯西黎曼方程。 

Riemann的主要研究方向是几何和分析，他一生一共只发表了10篇论文，但每一篇几乎都给所在领域带来了长足的进展和突破。他如今最广为大众所知的一篇，是在1859年提交的《论小于给定值的素数个数》，这似乎是与他的主要研究方向偏离最远的一篇论文。 

Riemann 

当时大学教授的名额有限，先是Gauss于1855年去世，由Dirichlet接任，之后Dirichlet也离开了，这个职务自然就落到了已经硕果累累Riemann的头上。 

这是1859年，柏林科学院决定授予他通讯院士，并鼓励他再写一篇论文来“使他的杰出成果获得正式承认”。没过多久，Riemann就提交了一篇名为《论小于给定值的素数个数》的这篇论文，一篇足足让后人魂牵梦萦近两百年的杰作。 

Riemann手稿 

论文的开头是这样的：“承蒙（柏林）科学院接纳我为通讯院士，我想表达被赐予这份殊荣的感谢之情的最好方式是立即利用由此得到的许可向其通报一项关于素数分布密度的研究，考虑到高斯和狄利克雷曾长期对此问题抱有浓厚的兴趣，它似乎并不是完全配不上这样性质的一个报告。

我以欧拉的发现、即下面这个等式作为本研究的起点[啊：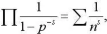

其中等式左边的p取遍所有质数，等式右边的n取遍所有正整数，我将用ζ(s)表记由上面这两个级数（当它们收敛时）表示的复变量s的函数。” 

ζ(s)就是大名鼎鼎的黎曼zeta函数。之后的内容Riemann专注于采用在复平面上围道积分来处理ζ(s)，以获得更好的性质。显然ζ(s)在复平面上很多地方是不收敛的。但Riemann将其解析延拓后使得ζ(s)在除了1这个单一极点外均有定义。经过一系列操作后ζ(s)满足以下方程：

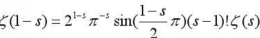
所以可以看到当1-s是负偶数时，右边式子显然为0，所以我们把负偶数叫做ζ(s)的平凡零点。Riemann在文中构造了一些新的函数来联系ζ(s)和π(x),并猜想了ζ函数的一系列性质。其中大部分都已被证明，只留下一条，那就是ζ(s)的所有非平凡零点的实部均为1/2，这也就是著名的Riemann猜想。 

或许Riemann当时已经意识到这个问题的复杂程度，他在文中写道：“对此我们自然希望能有一个严格的证明，然而在一些仓促的不成功的初步尝试之后，我暂时把寻求证明搁在一边，因为对于我接下来研究的目的来说它并不是必需的。” 

Riemann墓碑，上书： 

“万事都互相效力 

叫爱神的人得益处” 

那么找到ζ(s)的零点特点有什么意义呢？打个简单的比方，实数域有限次多项式如果知道它的所有零点，那么它可以简单地表示为一些一次和二次因式子的乘积。如果我们能证明Riemann猜想，那么ζ(s)就能很好地刻画，加上之前的一些工作，π(x)就能估计到非常精确。 

百余年的努力 

在最开始的三四十年中，Riemann的这个猜想没引起太多的反响。直到1896年，Hadamard等人用这篇论文中的思路和一些结果证明了素数定理，人们才开始广泛地关注这篇论文，以及其中留下待进一步证明的一个个猜想。 

一个关于英国数学大师Hardy的著名轶事就是一次他要乘船渡过波涛汹涌的英吉利海峡时，他给他的好友寄了一张明信片，上面写着：我已证明了Riemann猜想。“这样上帝就不舍得让我死了，否则我可以永垂青史。” 

Hardy 

Hardy确实做了第一个吃螃蟹的人，在1914年，他证明了Riemann ζ函数有无穷多个零点实部为1/2。然后Littlewood在七年之后证明了，在限定虚部大小的前提下，ζ的零点实部为1/2占满足条件零点一个正的比例。 

1942年，Selberg证明了对于全体的零点，其中实部为1/2的至少占了总数的千分之一。那么接下来只需把这个比例提高到100%。但直到1974年，Levinson才将其提升到三分之一。至今这个比例仍未超过一半。 

Selberg 

Gauss说：“数论是数学的皇后。”在数论领域，很多描述简单的猜想，例如Fermat大定理、Goldbach猜想等等，却是数学发展史上最硬的石头。正因为如此，这些猜想才妇孺皆知。 

由于Riemann猜想看上去如此的巧妙，而且几十年来在计算机上验证到前十万亿个零点猜想都是成立的，很多人更愿意相信这个猜想是正确的，于是就有了“如果RH(Riemann Hypothesis)成立”这个有趣的数学分支。 

至今这座理想的大厦已入驻了千余条数学命题，但地基还是不够牢固。一旦RH被证明，这一千多条命题都能荣升为定理：否则，随着大楼的轰然倒塌，相当一部分命题将一同陪葬。 

Riemann猜想证明主要思路 

Fermat定理于1995年被Andrew Wiles最终证明，Goldbach猜想目前最好的成果是陈景润于1973证明的“1+2”，与猜想要求的“1+1”近在咫尺，但也可能咫尺天涯。与前几天放出的风声一致，Riemann猜想的超级简短的证明的主要步骤昨日已由Michael Atiyah[注3]正式公布，主要思路仅仅只占了一页PPT。 

Atiyah的证明中的相关细节有待进一步审查，让我们继续拭目以待。 

可惜老爷子好像先走了~~