本文转自CSDN 写代码的柯长的博客
最近在研究graph learning,自然在接触到前沿的,自然学习到了超图学习。特在此做下记录:
hypergraph learning的主要论文来自:
Learning with Hypergraphs: Clustering, Classification, and Embedding
Learning Hypergraph-regularized Attribute Predictors
hypergraph
在说超图之前,希望先交待一下我们使用graph是出于怎样的考虑。我们只知道general graph的边是连接两点之前的一条边。那么,利用general graph更关心的是样本点与样本点之间的关系,是pairwise之间的关系。但是,在实际生活中,以及再做图像识别的领域中,我们需要关系的不仅仅是两点之间的关系,可能更要关心的是一个样本点与其他一类样本点之间的关系。这种复杂的关系是general graph所无法描绘出来的。更常见的例子,就是在论文发表的过程中,一篇论文如果只有一个作者,那我们则可以使用general graph来进行描述。但是当一篇论文如果有多个作者的时候,描述科研人员之间的合作关系的时候,使用general graph就有些力不从心。这时候,我们就可以使用超图这描述这样的关系,关于hypergraph 和graph有什么区别和联系,这里我上一张图来进行描述:
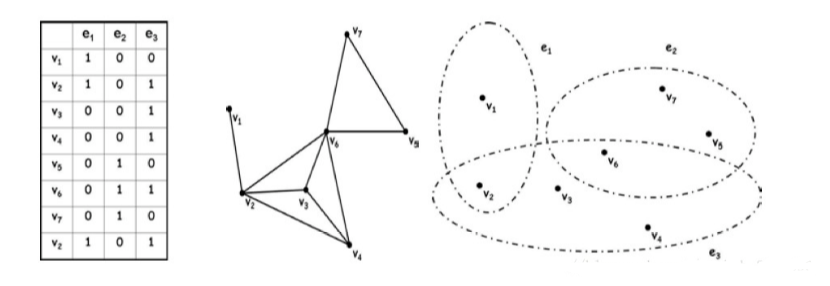
左边的表说明的是点与边之间的关系。中间的图说明的是general graph,右边的图是我们的hypergraph(每一个圈圈住的点的集合就是我们的hyperedge)。可以看出hypergraph强调的更多是集合的概念,一个hyperedge更多说明的是许多点的集合, 我们的general graph的edge说明的是两点之间的关系。在图像识别中,我们就可以认为图像的每一个属性都是一个hyperedge,hyperedge重叠的部分就是图像相同的属性,重叠部分越多说明两个sample 是同一类的可能性越大。
既然有了hypergraph,我们就要重新定义一些有关图的东西: δ(e)表示每一个hyperedge中的包含的顶点个数。
接下来就是,hyperedge的边权如何定义,我们利用heat kernel 来计算hyperedge集合中点与点之间的距离,然后求一个平均,得到的就是这个hyperedge的边权,公式如下:
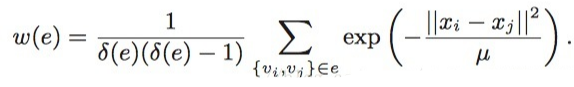
使用我们的hypergraph可以尽可能的描述样本点与整个样本数据的属性关系,只能当属性(超边)重叠多的时候才可以说明两个样本是属于通一类,它避免了只比较两个数据样本相似性的缺陷。
hypergraph的梗概部分完了,接下来我们来说说hypergraph learning
Hypergraph Learning
Hypergraph Learning。因为是Learning,我们自然要定义我们的loss function,根据我们做Normalized Cut的目标函数:让同类的的相关性尽可能大,不同类的相关性尽可能小。延伸到我们的hypergraph,便变成了我们的目标函数要尽可能的保持超边(样本的属性)关系。于是,就有了下面的目标函数:
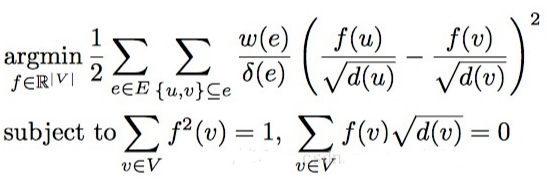
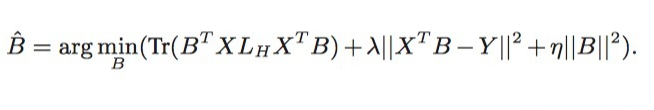
求解得到如下的答案:
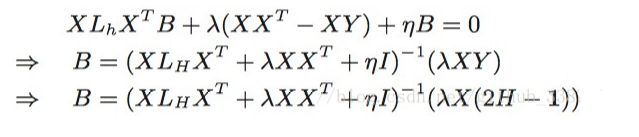
该贴被huang.wang编辑于2018-9-14 14:01:06


 技术讨论
技术讨论