本文转自 CSDN论坛一刀不二博客

在多指令流多数据流MIMD里面有用到基于超立方体互联的网络结构，

用《图论导引》里面简单的描述，就是处理器能通信，当且仅当他们的邻接（k元祖代表了处理器的地址）

一个 k 维立方体（或者超立方体Qk）是一种简单图，每个顶点{0,1}标记的k元祖来表示。

相邻的顶点之间的 k 元祖只有一个位置上数字不同，Qk 的生成立方体 Qj 和 Qj 本身同构。

这是Q3的表示：

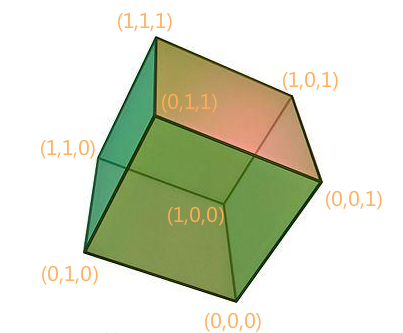
仔细观察会发现，Qk图里面的每条边链接的两个顶点的k元祖里的1的个数一端是奇数，另一端为偶数，

因此包含奇数个数 1 的点可以当做一个集合，偶数的也可以，所以 Qk 为二分图。

显而易见 Qk 有 2^k个顶点，每个顶点度为 k ，那么 Qk 里面会有 k* (2^k) / 2 条边。

Qk 里面有多少个 Qj 呢？

那么到底什么是（ 1,1,0,0,1,0,.............,1 ） 呢？

想想也就是 k 维世界的坐标，那么隔绝掉一维或者几个维度，剩下的就是那个世界里的空间变化情况。

可以这样想，k 维度空间的世界里面固定 j 维，假设在这样 j 维的世界里面只生产拥有 j 个维度的事物，

也就是元祖里面还剩下 k - j 个元素没有被固定，每个 j 维世界都有 2^( k - j ) 个事物（ Qj ），

那么 Qk 里面就一共有 C( k，j ) * 2^( k - j ) 个 Qj。

（或者反过来说，如果想要得到一个Qj，只需要固定 k - j 个标识，而将剩下的 j 位，取遍 2^j，

得到2^j个顶点，和它们间相连的边，就是一个Qj）

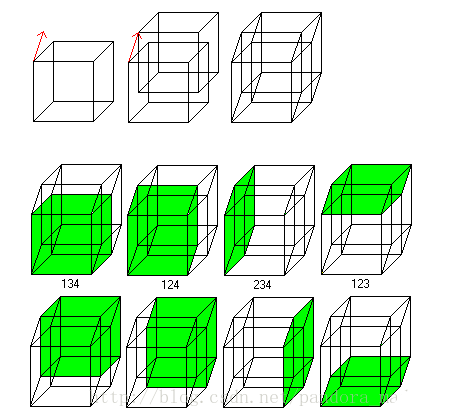
这是一个Q4图，Q4可以看做由一个Q3沿着某个维度移动一定距离，

然后将点对链接在一起得到的。里面有8 == C(4,3) * 2^1 个Q3（绿）。

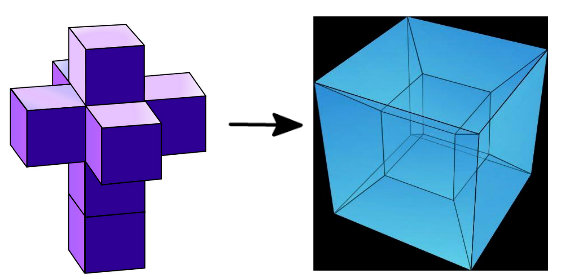
这也是Q4的另一种样子，如果你能想象出其由8个立方体叠在一起的话........

人的大脑里面并没有“厚度”的概念，所以只能通过数学的方式来理解高维空间的物体。

应用：

E-立方体路由算法

比如给定立方体中的起始点 s 和终止点 d，问从 s 到 d 的最短路径

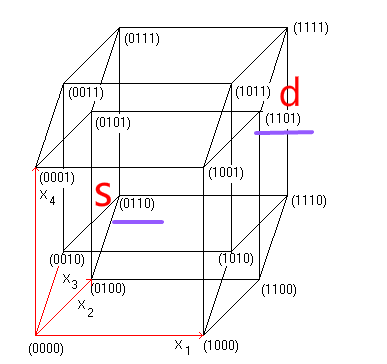
步骤：

1.计算方向位，r[i] = s[i-1] xor d[i-1]，其中i = 1，，，n

令 i = 1， v = s

2.若r[i] == 1，则从当前节点寻找下一节点 v xor 2^(i-1)

若r[i] == 0，跳过

3.i = i + 1，若 i <= n， 转2，否则退出

假设这里 s = 0110，d = 1101

step1.计算方位，r = s xor d = 1011

step2.因为 r[1] == 1，v = 0110 xor 0001 = 0111, i = 1

step3.因为 r[2] == 1，v = 0111 xor 0010 = 0101, i = 2

step4.因为 r[3] == 0，跳过 v = 0101， i = 3

step5.因为 r[4] == 1，v = 0101 xor 1000 = 1101 = d, i = 4, end

路径为 0110 -> 0111 -> 0101 -> 1101