本文转自 CSDN博客

一、动态规划初探

1、递推

暂且先不说动态规划是怎么样一个算法，由最简单的递推问题说起应该是最恰当不过得了。因为一来，递推的思想非常浅显，从初中开始就已经有涉及，等差数列f[i]=f[i-1]+d（i>0，d为公差，f[0]为初项）就是最简单的递推公式之一；二来，递推作为动态规划的基本方法，对理解动态规划起着至关重要的作用。理论的开始总是枯燥的，所以让读者提前进入思考是最能引起读者兴趣的利器，于是【例题1】应运而生。

【例题1】在一个3XN的长方形方格中，铺满1X2的骨牌（骨牌个数不限制），给定N，求方案数（图一-1-1为N=2的所有方案），所以N=2时方案数为3。

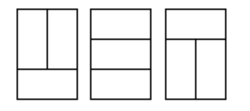
图一-1-1

这是一个经典的递推问题，如果觉得无从下手，我们可以来看一个更加简单的问题，把问题中的“3”变成“2”（即在一个2XN的长方形方格中铺满1X2的骨牌的方案）。这样问题就简单很多了，我们用f[i]表示2Xi的方格铺满骨牌的方案数，那么考虑第i列，要么竖着放置一个骨牌；要么连同i-1列，横着放置两个骨牌，如图2所示。由于骨牌的长度为1X2，所以在第i列放置的骨牌无法影响到第i-2列。很显然，图一-1-2中两块黑色的部分分别表示f[i-1]和f[i-2]，所以可以得到递推式f[i]=f[i-1]+f[i-2](i>=2)，并且边界条件f[0]=f[1]=1。

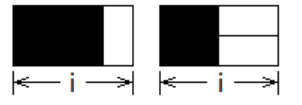
图一-1-2

再回头来看3XN的情况，首先可以明确当N等于奇数的时候，方案数一定为0。所以如果用f[i](i为偶数)表示3Xi的方格铺满骨牌的方案数，f[i]的方案数不可能由f[i-1]递推而来。那么我们猜想f[i]和f[i-2]一定是有关系的，如图一-1-3所示，我们把第i列和第i-1列用1X2的骨牌填满后，轻易转化成了f[i-2]的问题，那是不是代表f[i]=3*f[i-2]呢？

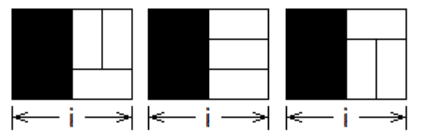
图一-1-3

仔细想想才发现不对，原因是我们少考虑了图一-1-4的情况，这些情况用图一-1-3的情况无法表示，再填充完黑色区域后，发现和f[i-4]也有关系，但是还是漏掉了一些情况。

图一-1-4

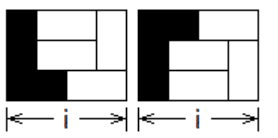
上面的问题说明我们在设计状态（状态在动态规划中是个很重要的概念，在本章的第4小节会进行介绍总结）的时候的思维定式，当一维的状态已经无法满足我们的需求时，我们可以试着增加一维，用二维来表示状态，用f[i][j]表示(3Xi)+j个多余块的摆放方案数，如图一-1-5所示：

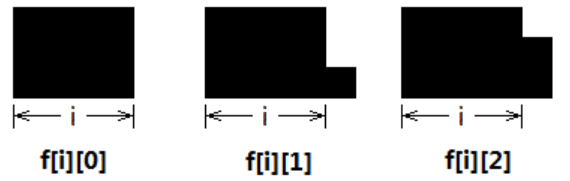
图一-1-5

转化成二维后，我们可以轻易写出三种情况的递推式，具体推导方法见图一-1-6。

f[i][0]=f[i-2][0]+f[i-1][1]+f[i-2][2]

f[i][1]=f[i-1][2]

f[i][2]=f[i][0]+f[i-1][1]

边界条件f[0][0]=f[1][1]=f[0][2]=1

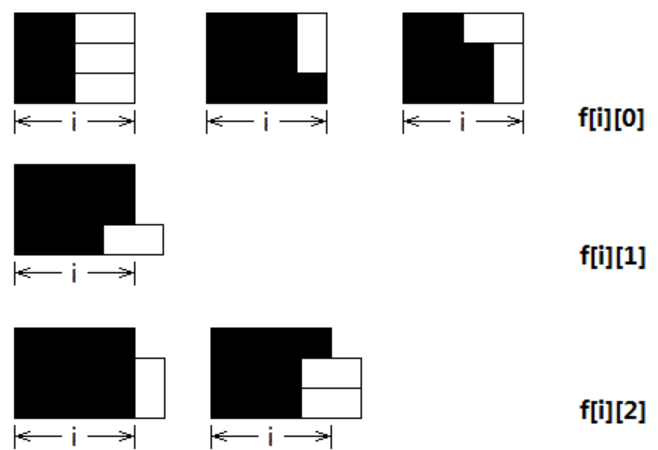
图一-1-6

如果N不是很大的情况，到这一步，我们的问题已经完美解决了，其实并不需要求它的通项公式，因为我们是程序猿，一个for循环就能搞定了<*_*>，接下来的求解就全仰仗于计算机来完成了。

【例题2】对一个“01”串进行一次μ变换被定义为：将其中的"0"变成"10"，"1"变成"01"，初始串为"1"，求经过N(N<=1000)次μ变换后的串中有多少对"00"（有没有人会纠结会不会出现"000"的情况？这个请放心，由于问题的特殊性，不会出现"000"的情况）。图一-1-7表示经过小于4次变换时串的情况。

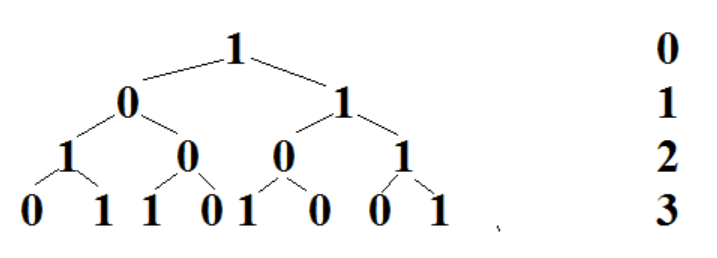
图一-1-7

如果纯模拟的话，每次μ变换串的长度都会加倍，所以时间和空间复杂度都是O(2^n)，对于n为1000的情况，完全不可能计算出来。仔细观察这个树形结构，可以发现要出现"00"，一定是"10"和"01"相邻产生的。为了将问题简化，我们不妨设A="10",B="01"，构造出的树形递推图如图一-1-8所示，如果要出现"00"，一定是AB（"1001"）。

令FA[i]为A经过i次μ变换后"00"的数量，FA[0]=0;FB[i]为B经过i次μ变换后"00"的数量，FB[0]=0。

从图中观察得出，以A为根的树，它的左子树的最右端点一定是B，也就是说无论经过多少次变换，两棵子树的交界处都不可能产生AB，所以FA[i]=FB[i-1]+FA[i-1]（直接累加两棵子树的"00"的数量）；而以B为根的树，它的左子树的右端点一定是A，而右子树的左端点呈BABABA...交替排布，所以隔代产生一次AB，于是FB[i]=FA[i-1]+FB[i-1]+(imod2)。最后要求的答案就是FB[N-1]，递推求解。

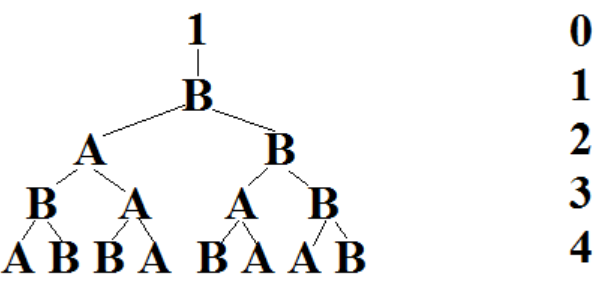
图一-1-8

2、记忆化搜索

递推说白了就是在知道前i-1项的值的前提下，计算第i项的值，而记忆化搜索则是另外一种思路。它是直接计算第i项，需要用到第j项的值(j<i)时去查表，如果表里已经有第j项的话，则直接取出来用，否则递归计算第j项，并且在计算完毕后把值记录在表中。记忆化搜索在求解多维的情况下比递推更加方便，【例题3】是我遇到的第一个记忆化搜索的问题，记忆犹新。

【例题3】这个问题直接给出了一段求函数w(a,b,c)的伪代码：

要求给定a,b,c，求w(a,b,c)的值。

乍看下只要将伪代码翻译成实际代码，然后直接对于给定的a,b,c，调用函数w(a,b,c)就能得到值了。但是只要稍加分析就能看出这个函数的时间复杂度是指数级的（尽管这个三元组的最大元素只有20，这是个陷阱）。对于任意一个三元组(a,b,c)，w(a,b,c)可能被计算多次，而对于固定的(a,b,c)，w(a,b,c)其实是个固定的值，没必要多次计算，所以只要将计算过的值保存在f[a][b][c]中，整个计算就只有一次了，总的时间复杂度就是O(n^3)，这个问题的n只有20。

3、状态和状态转移

在介绍递推和记忆化搜索的时候，都会涉及到一个词---状态，它表示了解决某一问题的中间结果，这是一个比较抽象的概念，例如【例题1】中的f[i][j]，【例题2】中的FA[i]、FB[i]，【例题3】中的f[a][b][c]，无论是递推还是记忆化搜索，首先要设计出合适的状态，然后通过状态的特征建立状态转移方程（f[i]=f[i-1]+f[i-2]就是一个简单的状态转移方程）。

4、最优化原理和最优子结构

在介如果问题的最优解包含的子问题的解也是最优的，就称该问题具有最有子结构，即满足最优化原理。这里我尽力减少理论化的概念，而改用一个简单的例题来加深对这句话的理解。

【例题4】给定一个长度为n(1<=n<=1000)的整数序列a[i]，求它的一个子序列(子序列即在原序列任意位置删除0或多个元素后的序列)，满足如下条件：

1、该序列单调递增；

2、在所有满足条件1的序列中长度是最长的；

这个问题是经典的动态规划问题，被称为最长单调子序列。

我们假设现在没有任何动态规划的基础，那么看到这个问题首先想到的是什么？

我想到的是万金油算法---枚举（DFS），即枚举a[i]这个元素取或不取，所有取的元素组成一个合法的子序列，枚举的时候需要满足单调递增这个限制，那么对于一个n个元素的序列，最坏时间复杂度自然就是O(2n)，n等于30就已经很变态了更别说是1000。但是方向是对的，动态规划求解之前先试想一下搜索的正确性，这里搜索的正确性是很显然的，因为已经枚举了所有情况，总有一种情况是我们要求的解。我们尝试将搜索的算法进行一些改进，假设第i个数取的情况下已经搜索出的最大长度记录在数组d中，即用d[i]表示当前搜索到的以a[i]结尾的最长单调子序列的长度，那么如果下次搜索得到的序列长度小于等于d[i]，就不必往下搜索了（因为即便继续往后枚举，能够得到的解必定不会比之前更长）；反之，则需要更新d[i]的值。如图一-4-1，红色路径表示第一次搜索得到的一个最长子序列1、2、3、5，蓝色路径表示第二次搜索，当枚举第3个元素取的情况时，发现以第3个数结尾的最长长度d[3]=3，比本次枚举的长度要大（本次枚举的长度为2），所以放弃往下枚举，大大减少了搜索的状态空间。

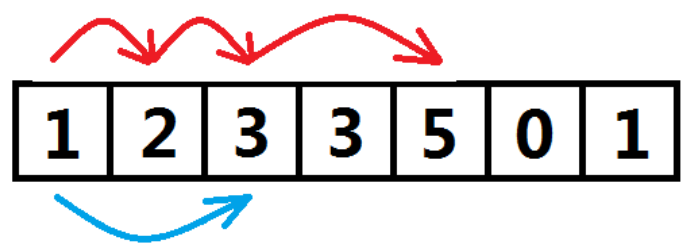
图一-4-1

这时候，我们其实已经不经意间设计好了状态，就是上文中提到的那个d[i]数组，它表示的是以a[i]结尾的最长单调子序列的长度，那么对于任意的i，d[i]一定等于d[j]+1(j<i)，而且还得满足a[j]<a[i]。因为这里的d[i]表示的是最长长度，所以d[i]的表达式可以更加明确，即：

d[i]=max{d[j]|j<i&&a[j]<a[i]}+1

这个表达式很好的阐释了最优化原理，其中d[j]作为d[i]的子问题，d[i]最长（优）当且仅当d[j]最长（优）。当然，这个方程就是这个问题的状态转移方程。状态总数量O(n),每次转移需要用到前i项的结果，平摊下来也是O(n)的,所以该问题的时间复杂度是O(n^2)，然而它并不是求解这类问题的最优解，下文会提到最长单调子序列的O(nlogn)的优化算法。

5、决策和无后效性

一个状态演变到另一个状态，往往是通过“决策”来进行的。有了“决策”，就会有状态转移。而

无后效性，就是一旦某个状态确定后，它之前的状态无法对它之后的状态产生“效应”（影响）。

【例题5】老王想在未来的n年内每年都持有电脑，m(y,z)表示第y年到第z年的电脑维护费用，其中y的范围为[1,n]，z的范围为[y,n]，c表示买一台新的电脑的固定费用。给定矩阵m，固定费用c，求在未来n年都有电脑的最少花费。

考虑第 i 年是否要换电脑，换和不换是不一样的决策，那么我们定义一个二元组(a, b)，其中 a < b，它表示了第a年和第b年都要换电脑（第a年和第b年之间不再换电脑），如果假设我们到第a年为止换电脑的最优方案已经确定，那么第a年以前如何换电脑的一些列步骤变得不再重要，因为它并不会影响第b年的情况，这就是无后效性。

更加具体得，令d[i]表示在第i年买了一台电脑的最小花费(由于这台电脑能用多久不确定，所以第i年的维护费用暂时不计在这里面)，如果上一次更换电脑的时间在第j年，那么第j年更换电脑到第i年之前的总开销就是c + m(j, i-1)，于是有状态转移方程：

d[i] = min{ d[j] + m(j, i-1) |  1 <=  j < i  } + c

这里的d[i]并不是最后问题的解，因为它漏算了第i年到第n年的维护费用，所以最后问题的答案：

ans  = min{ d[i] + m(i, n)  | 1 <= i < n }

我们发现两个方程看起来很类似，其实是可以合并的，我们可以假设第n+1年必须换电脑，并且第n+1年换电脑的费用为0，那么整个阶段的状态转移方程就是：

d[i] = min{ d[j] + m(j, i-1) | 1 <= j < i } + w(i)    其中w(i) = (i==n+1)?0:c;

d[n+1]就是我们需要求的最小费用了。

二、动态规划的经典模型

1、线性模型

线性模型的是动态规划中最常用的模型，上文讲到的最长单调子序列就是经典的线性模型，这里的线性指的是状态的排布是呈线性的。【例题6】是一个经典的面试题，我们将它作为线性模型的敲门砖。

【例题6】在一个夜黑风高的晚上，有n（n<=50）个小朋友在桥的这边，现在他们需要过桥，但是由于桥很窄，每次只允许不大于两人通过，他们只有一个手电筒，所以每次过桥的两个人需要把手电筒带回来，i号小朋友过桥的时间为T[i]，两个人过桥的总时间为二者中时间长者。问所有小朋友过桥的总时间最短是多少。

图二-1-1

每次过桥的时候最多两个人，如果桥这边还有人，那么还得回来一个人（送手电筒），

也就是说N个人过桥的次数为2*N-3（倒推，当桥这边只剩两个人时只需要一次，三个人的情况为来回一次后加上两个人的情况...）。

有一个人需要来回跑，将手电筒送回来（也许不是同一个人，realy？！）

这个回来的时间是没办法省去的，并且回来的次数也是确定的，为N-2，如果是我，我会选择让跑的最快的人来干这件事情，但是我错了...

如果总是跑得最快的人跑回来的话，那么他在每次别人过桥的时候一定得跟过去，于是就变成就是很简单的问题了，

花费的总时间：T=minPTime*(N-2)+(totalSum-minPTime)

来看一组数据四个人过桥花费的时间分别为12510，按照上面的公式答案是19，但是实际答案应该是17。

具体步骤是这样的：

第一步：1和2过去，花费时间2，然后1回来（花费时间1）；

第二歩：3和4过去，花费时间10，然后2回来（花费时间2）；

第三部：1和2过去，花费时间2，总耗时17。

所以之前的贪心想法是不对的。

我们先将所有人按花费时间递增进行排序，

假设前i个人过河花费的最少时间为opt[i]，

那么考虑前i-1个人过河的情况，即河这边还有1个人，河那边有i-1个人，并且这时候手电筒肯定在对岸，所以

opt[i]=opt[i-1]+a[1]+a[i](让花费时间最少的人把手电筒送过来，然后和第i个人一起过河)

如果河这边还有两个人，一个是第i号，另外一个无所谓，河那边有i-2个人，并且手电筒肯定在对岸，所以

opt[i]=opt[i-2]+a[1]+a[i]+2*a[2](让花费时间最少的人把电筒送过来，然后第i个人和另外一个人一起过河，由于花费时间最少的人在这边，所以下一次送手电筒过来的一定是花费次少的，送过来后花费最少的和花费次少的一起过河，解决问题)

所以opt[i]=min{opt[i-1]+a[1]+a[i],opt[i-2]+a[1]+a[i]+2*a[2]}

2、区间模型

区间模型的状态表示一般为d[i][j]，表示区间[i,j]上的最优解，然后通过状态转移计算出[i+1,j]或者[i,j+1]上的最优解，逐步扩大区间的范围，最终求得[1,len]的最优解。

【例题7】给定一个长度为n（n<=1000）的字符串A，求插入最少多少个字符使得它变成一个回文串。

典型的区间模型，回文串拥有很明显的子结构特征，即当字符串X是一个回文串时，在X两边各添加一个字符'a'后，aXa仍然是一个回文串，我们用d[i][j]来表示A[i...j]这个子串变成回文串所需要添加的最少的字符数，那么对于A[i]==A[j]的情况，很明显有d[i][j]=d[i+1][j-1]（这里需要明确一点，当i+1>j-1时也是有意义的，它代表的是空串，空串也是一个回文串，所以这种情况下d[i+1][j-1]=0）；当A[i]!=A[j]时，我们将它变成更小的子问题求解，我们有两种决策：

1、在A[j]后面添加一个字符A[i]；

2、在A[i]前面添加一个字符A[j]；

根据两种决策列出状态转移方程为：

d[i][j]=min{d[i+1][j],d[i][j-1]}+1;(每次状态转移，区间长度增加1)

空间复杂度O(n^2)，时间复杂度O(n^2)，下文会提到将空间复杂度降为O(n)的优化算法。

3、背包模型

背包问题是动态规划中一个最典型的问题之一。由于网上有非常详尽的背包讲解

，这里只将常用部分抽出来，具体推导过程详见《背包九讲》。

a.0/1背包

有N种物品（每种物品1件）和一个容量为V的背包。放入第i种物品耗费的空间是Ci，得到

的价值是Wi。求解将哪些物品装入背包可使价值总和最大。

f[i][v]表示前i种物品恰好放入一个容量为v的背包可以获得的最大价值。

决策为第i个物品在前i-1个物品放置完毕后，是选择放还是不放，状态转移方程为：

f[i][v]=max{f[i-1][v],f[i-1][v-Ci]+Wi}

时间复杂度O(VN)，空间复杂度O(VN)（空间复杂度可利用滚动数组进行优化达到O(V)，下文会介绍滚动数组优化）。

b.完全背包

有N种物品（每种物品无限件）和一个容量为V的背包。放入第i种物品耗费的空间是Ci，得到的价值是Wi。求解将哪些物品装入背包可使价值总和最大。

f[i][v]表示前i种物品恰好放入一个容量为v的背包可以获得的最大价值。

f[i][v]=max{f[i-1][v-kCi]+kWi|0<=k<=v/Ci

}(当k的取值为0,1时，这就是01背包的状态转移方程）

时间复杂度O(VNsum{V/Ci})，空间复杂度在用滚动数组优化后可以达到O(V)。

进行优化后（此处省略500字），状态转移方程变成：f[i][v]=max{f[i-1][v],f[i][v-Ci]+Wi}

时间复杂度降为O(VN)。

c.多重背包

有N种物品（每种物品Mi件）和一个容量为V的背包。放入第i种物品耗费的空间是Ci，得到的价值是Wi。求解将哪些物品装入背包可使价值总和最大。

f[i][v]表示前i种物品恰好放入一个容量为v的背包可以获得的最大价值。f[i][v]=max{f[i-1][v-kCi]+kWi|0<=k<=Mi}

时间复杂度O(Vsum(Mi))，空间复杂度仍然可以用滚动数组优化后可以达到O(V)。

优化：采用二进制拆分物品，将Mi个物品拆分成容量为1、2、4、8、...2^k、Mi-(2^(k+1)-1)个对应价值为Wi、2Wi、4Wi、8Wi、...、2^kWi、（

Mi-(2^(k+1)-1)

）Wi的物品，然后采用01背包求解。

这样做的时间复杂度降为O(Vsum(logMi))。

【例题8】一群强盗想要抢劫银行，总共N(N<=100)个银行，第i个银行的资金为Bi亿，抢劫该银行被抓概率Pi，问在被抓概率小于p的情况下能够抢劫的最大资金是多少？

p表示的是强盗在抢银行时至少有一次被抓概率的上限，那么选择一些银行，并且计算抢劫这些银行都不被抓的的概率pc，则需要满足1-pc<p。这里的pc是所有选出来的银行的抢劫时不被抓概率（即1-Pi）的乘积，于是我们用资金作为背包物品的容量，概率作为背包物品的价值，求01背包。状态转移方程为：

f[j]=max{f[j],f[j-pack[i].B]*(1-pack[i].p)}

最后得到的f[i]表示的是抢劫到i亿资金的最大不被抓概率。令所有银行资金总和为V，那么从V-0进行枚举，第一个满足1-f[i]<p的i就是我们所要求的被抓概率小于p的最大资金。

4、状态压缩模型

状态压缩的动态规划，一般处理的是数据规模较小的问题，将状态压缩成k进制的整数，k取2时最为常见。

【例题9】对于一条n(n<=11)个点的哈密尔顿路径C1C2...CN（经过每个点一次的路径）的值由三部分组成：

1、每个顶点的权值Vi的和

2、对于路径上相邻的任意两个顶点CiCi+1，累加权值乘积Vi*Vi+1

3、对于相邻的三个顶点CiCi+1Ci+2，如果Ci和Ci+2之间有边，那么累加权值三乘积Vi*Vi+1*Vi+2

求值最大的哈密尔顿路径的权值和这样的路径的个数。

枚举所有路径，判断找出值最大的，复杂度为O(n！)，取缔！

由于点数较少，采用二进制表示状态，用d[i][j][k]表示某条哈密尔顿路径的最大权值，其中i是一个二进制整数，它的第t位为1表示t这个顶点在这条哈密尔顿路径上，为0表示不在路径上。j和k分别为路径的最后两个顶点。那么图二-4-1表示的状态就是：

d[(11101111)2][7][1]

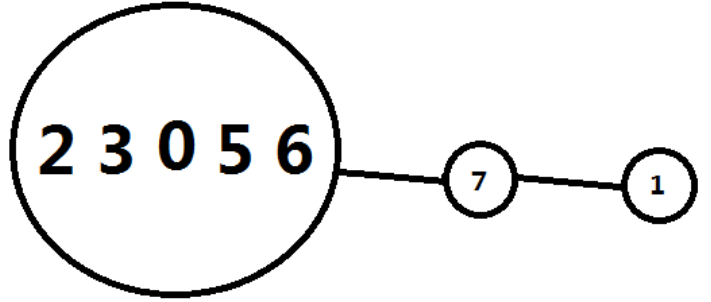
图二-4-1

明确了状态表示，那么我们假设02356这5个点中和7直接相连的是i，于是就转化成了子问题...->j->i->7，我们可以枚举i=0，2，3，5，6。

直接给出状态转移方程：

d[i][j][k]=max{d[i^(1<<k)][t][j]+w(t,j,k)|(i&(1<<t))!=0}

这里用到了几个位运算:i^(1<<k)表示将i的二进制的第k位从1变成0，i&(1<<t)则为判断i的二进制表示的第t位是否为1，即该路径中是否存在t这个点。这个状态转移的实质就是将原本的...->j->k转化成更加小规模的去掉k点后的子问题...->t->j求解。而w(t,j,k)则表示t->j->k这条子路径上产生的权值和，这个可以由定义在O(1)的时间计算出来。

d[(1<<j)|(1<<k)][j][k]为所有的两个点的路径的最大值，即最小的子问题。这个问题的状态并非线性的，所以用记忆化搜索来求解状态的值会事半功倍。

【例题10】

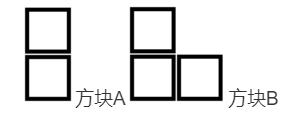
利用以上两种积木（任意数量，可进行旋转和翻转），拼出一个m*n(1<=m<=9,1<=n<=9)的矩形，问这样的方式有多少种。如m=2,n=3的情况，有以下5种拼接方式：

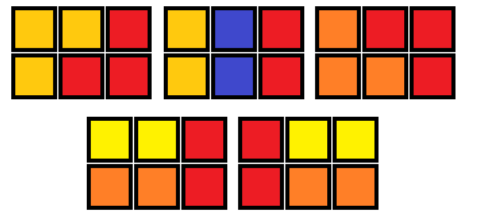
图二-4-2

经典问题，2进制状态压缩。有固定套路，就不纠结是怎么想出来的了，反正第一次看到这种问题我是想不出来，你呢？但是照例还是得引导一下。

如果问题不是求放满的方案数，而是求前M-1行放满，并且第M行的奇数格放上骨牌而偶数格不放或者第M行有一个格子留空或者第M行的首尾两个格子留空，求方案数（这是三个问题，分别对应图二-4-3的三个图）。这样的问题可以出一箩筐了，因为第M行的情况总共有2^n，按照这个思路下去，我们发现第i(1<=i<=m)行的状态顶多也就2^n

种，这里的状态可以用一个二进制整数来表示，对于第i行，如果这一行的第j个格子被骨牌填充则这个二进制整数的第j位为1，否则为0。

图二-4-3中的三个图的第M行状态可以分别表示为(101010)2、(110111)2、(011110)2，那么如果我们已知第i行的状态k对应的方案数，并且状态k放置几个骨牌后能够将i+1行的状态变成k'，那么第i+1行的k'这个状态的方案数必然包含了第i行的状态k的方案数，这个放置骨牌的过程就是状态转移。

图二-4-3

用一个二维数组DP[i][j]表示第i行的状态为j的骨牌放置方案数(其中1<=i<=m,0<=j<2n)，为了将问题简化，我们虚拟出一个第0行，则有DP[0][j]=(j==2n-1)?1:0；这个就是我们的初始状态，它的含义是这样的，因为第0行是我们虚拟出来的，所以第0行只有完全放满的时候才有意义，也就是第0行全部放满（状态的二进制表示全为1，即十进制表示的2n-1）的方案数为1，其它情况均为0。

那么如何进行状态转移呢？假设第3行的某个状态(101000)2的方案数DP[3][(101000)2]=5，如图二-4-4所示：

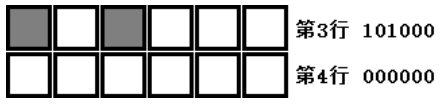
图二-4-4

我们需要做的就是通过各种方法将第3行填满，从而得到一系列第4行可能的状态集合S，并且对于每一个在S中的状态s，执行DP[4][s]+=DP[3][(101000)2]（两个状态可达，所以方案数是可传递的，又因为多个不同的状态可能到达同一个状态，所以采用累加的方式）。

根据给定的骨牌，我们可以枚举它的摆放方式，图二-4-5展示了三种骨牌的摆放方式以及能够转移到的状态，但是这里的状态转移还没结束，因为第3行尚未放满，问题求的是将整个棋盘铺满的方案数，所以只有当第i行全部放满后，才能将状态转移给i+1行。

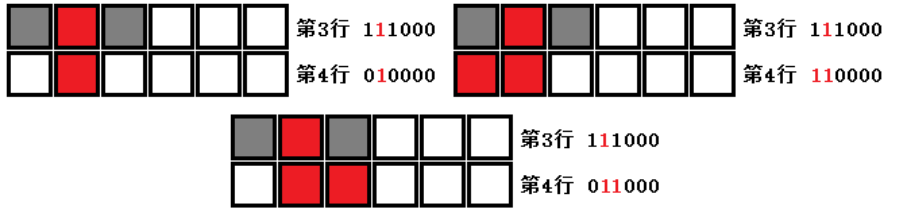
图二-4-5

枚举摆放的这一步可以采用dfs递归枚举列，递归出口为列数col==N时。dfs函数的原型可以写成如下的形式：

voiddfs(intcol,intnextrow,intnowstate,intnextstate,LLcnt);

//col表示当前枚举到的列编号

//nextrow表示下一行的行编号

//nowstate表示当前枚举骨牌摆放时第i行的状态（随着放置骨后会更新）

//nextstate表示当前枚举骨牌摆放时第i+1行的状态（随着放置骨后会更新）

//cnt状态转移前的方案数，即第i行在放置骨牌前的方案数

然后再来看如何将骨牌摆上去，这里对骨牌进行归类，旋转之后得到如下六种情况：

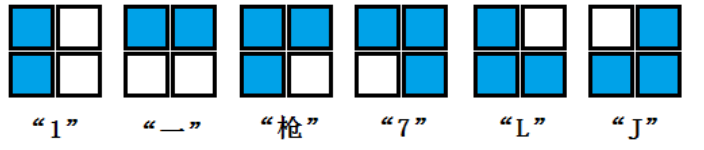
图二-4-6

图二-4-7

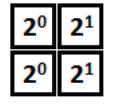
为了方便叙述，分别给每个类型的骨牌强加了一个奇怪的名字，都是按照它自身的形状来命名的，o(╯□╰)o。然后我们发现它们都被圈定在一个2X2的格子里，所以每个骨牌都可以用2个2位的2进制整数来表示，编码方式类似上面的状态表示法（参照图6，如果骨牌对应格子为蓝色则累加格子上的权值），定义如下：

blockMask[k][0]表示骨牌第一行的状态，blockMask[k][1]表示骨牌第二行的状态。这样一来就可以通过简单的位运算来判断第k块骨牌是否可以放在(i,col)这个格子上，这里的i表示行编号，col则表示列编号。接下来需要用到位运算进行状态转移，所以先介绍几种常用的位运算：

a.x&(1<<i)值如果非0，表示x这个数字的二进制表示的第i(i>=0)位为1，否则为0；

b.x&(y<<i)值如果非0，表示存在一个p(i<=p<i+k)，使得x这个数字的二进制表示的第p位和y的p-i位均为1（k为y的二进制表示的位数）；

c.x|(1<<i)将x的第i位变成1（当然，有可能原本就为1，这个不影响）；

d.x|(y<<i)将x的第i~i+k-1位和y进行位或运算（k为y的二进制表示的位数），这一步就是模拟了骨牌摆放；

那么这个格子可以放置第k个骨牌的条件有如下几个：

1、当前骨牌横向长度记为w，那么w必须满足col+w<=N，否则就超出右边界了。

2、nowstate&(blockMask[k][0]<<col)==0，即第i行，骨牌放入前对应的格子为空（对应的格子表示骨牌占据的格子，下同）

3、nextstate&(blockMask[k][1]<<col)==0，即第i+1行，骨牌放入前对应的格子为空

4、最容易忽略的一点是，“J”骨牌放置时，它的缺口部分之前必须要被骨牌铺满，否则就无法满足第i行全铺满这个条件了，如图二-4-8所示的情况。

图二-4-8

当四个条件都满足就可以递归进入下一层了，递归的时候也是采用位运算，实现如下：

dfs(col+1,nextrow,nowstate|(blockMask[k][0]<<col),nextstate|(blockMask[k][1]<<col),cnt);

这里的位或运算（|）就是模拟将一个骨牌摆放到指定位置的操作（参见位运算d）。

当然，在枚举到第col列的时候，有可能(i,col)这个格子已经被上一行的骨牌给“占据”了（是否被占据可以通过(1<<col)&nowstate得到），这时候我们只需要继续递归下一层，只递增col，其它量都不变即可，这表示了这个格子什么都不放的情况。

5、树状模型

树形动态规划（树形DP），是指状态图是一棵树，状态转移也发生在树上，父结点的值通过所有子结点计算完毕后得出。

【例题11】给定一颗树，和树上每个结点的权值，求一颗非空子树，使得权和最大。

用d[1][i]表示i这个结点选中的情况下，以i为根的子树的权和最大值;

用d[0][i]表示i这个结点不选中的情况下，以i为根的子树的权和最大值;

d[1][i]=v[i]+sum{d[1][v]|v是i的直接子结点&&d[1][v]>0}

d[0][i]=max(0,max{max(d[0][v],d[1][v])|v是i的直接子结点})

这样，构造一个以1为根结点的树，然后就可以通过dfs求解了。

这题题目要求求出的树为非空树，所以当所有权值都为负数的情况下需要特殊处理，选择所有权值中最大的那个作为答案。

三、动态规划的常用状态转移方程

动态规划算法三要素（摘自黑书，总结的很好，很有概括性）：

①所有不同的子问题组成的表

②解决问题的依赖关系可以看成是一个图

③填充子问题的顺序（即对②的图进行拓扑排序，填充的过程称为状态转移）；

 则如果子问题的数目为O(nt)，每个子问题需要用到O(ne)个子问题的结果，那么我们称它为tD/eD的问题，于是可以总结出四类常用的动态规划方程：

（下面会把opt作为取最优值的函数（一般取min或max）, w(j, i)为一个实函数，其它变量都可以在常数时间计算出来）。)

       1、1D/1D

             d[i] = opt{ d[j] + w(j, i) | 0 <= i < j } (1 <= i <= n)

             【例题4】和【例题5】都是这类方程。

       2、2D/0D

             d[i][j] = opt{ d[i-1][j] + xi, d[i][j-1] + yj, d[i-1][j-1] + zij }     (1<= i, j <= n)

             【例题7】是这类方程的变形，最典型的见最长公共子序列问题。

       3、2D/1D

              d[i][j] = w(i, j) + opt{ d[i][k-1] + d[k][j] }, (1 <= i < j <= n)

               区间模型常用方程。

               另外一种常用的2D/1D的方程为：

              d[i][j] = opt{ d[i-1][k] + w(i, j, k) | k < j }    (1<= i <= n, 1 <= j <= m)

       4、2D/2D

             d[i][j] = opt{ d[i'][j'] + w(i', j', i, j) |  0 <= i' < i, 0 <= j' < j}

常见于二维的迷宫问题，由于复杂度比较大，所以一般配合数据结构优化，如线段树、树状数组等。

对于一个tD/eD 的动态规划问题，在不经过任何优化的情况下，可以粗略得到一个时间复杂度是O(nt+e)，空间复杂度是O(nt)的算法，大多数情况下空间复杂度是很容易优化的，难点在于时间复杂度，下一章我们将详细讲解各种情况下的动态规划优化算法。

四、动态规划和数据结构结合的常用优化

1、滚动数组

【例题12】例题7（回文串那题）的N变成5000，其余不变。回忆一下那个问题的状态转移方程如下：

       d[i][j] =   {

                                 d[i+1][j-1]                           | A[i] == A[j] 

                                 min{ d[i+1][j], d[i][j-1] } + 1  |  A[i] != A[j]

                      }

我们发现将d[i][j]理解成一个二维的矩阵，i表示行，j表示列，那么第i行的结果只取决于第i+1和第i行的情况，对于第i+2行它表示并不关心，那么我们只要用一个d[2][N]的数组就能保存状态了，其中d[0][N]为奇数行的状态值，d[1][N]为偶数行的状态值，当前需要计算的状态行数为奇数时，会利用到

d[1][N]的部分状态，奇数行计算完毕，

d[1][N]整行状态都没用了，可以用于下一行状态的保存，类似“传送带”的滚动来循环利用空间资源，美其名曰-滚动数组。

这是个2D/0D问题，理论的空间复杂度是O(n2)，利用滚动数组可以将空间降掉一维，变成O(n)。

背包问题的几个状态转移方程同样可以用滚动数组进行空间优化。

2、最长单调子序列

d[i]=max{d[j]|j<i&&a[j]<a[i]}+1;

那个问题的状态转移方程如下：

【例题13】例题4（最长递增子序列那题）的N变成100000，其余不变。

首先明确决策的概念，我们认为j和k(j<i,k<i)都是在计算d[i]时的两个决策。那么假设他们满足a[j]<a[k

]（它们的状态对应就是d[j]和d[k]），如果a[i]>a[k]，则必然有a[i]>a[j]，能够选k做决策的也必然能够选j做决策，那么如若此时d[j]>=d[k]，显然k不可能是最优决策（j的决策始终比它优，以j做决策，a[j]的值小但状态值却更大），所以d[k]是不需要保存的。

基于以上理论，我们可以采用二分枚举，维护一个值(这里的值指的是a[i])递增的决策序列，不断扩大决策序列，最后决策的数目就是最长递增子序列的长度。具体做法是：

枚举i，如果a[i]比决策序列中最大的元素的值还大，则将i插入到决策序列的尾部；否则二分枚举决策序列，找出其中值最小的一个决策k，并且满足a[k]>a[i]，然后用决策i替换决策k。

这是个1

D/1D问题，理论的时间复杂度是O(n2)，利用单调性优化后可以将复杂度将至O(nlogn)。

【例题14】给定n个元素(n<=100000)的序列，将序列的所有数分成x堆，每堆都是单调不增的，求x的最小值。

结论：可以转化成求原序列的最长递增子序列。

证明：因为这x堆中每堆元素都是单调不增的，所以原序列的最长递增子序列的每个元素在分出来的每堆元素中一定只出现最多一个，那么最长递增子序列的长度L的最大值为x，所以x>=L。

而我们要求的是x的最小值，于是这个最小值就是L了。

3、矩阵优化

【例题15】三个小岛，编号1、2、3，老王第0天在1号岛上。这些岛有一些奇怪的规则，每过1天，1号岛上的人必须进入2、3号岛；2号岛上的人必须进入1号岛；3号岛上的人可以前往1、2或留在3号岛

。问第n(n<=109)天老王在到达1号岛的行走方案，由于数据比较大，只需要输出ansMOD100000007的值即可。

图四-3-1

临时想的一个问题，首先看问题有几个维度，岛和天数，而且状态转移是常数级的，所以这是个2D/0D问题，我们用f[i][j]表示第i天在j号岛上的方案数，那么初始状态f[0][1]=1,f[0][2]=f[0][3]=0。

状态转移可以参考图四-3-1，有：

f[i][1]=f[i-1][2]+f[i-1][3]

f[i][2]=f[i-1][1]+f[i-1][3]

f[i][3]=f[i-1][1]+f[i-1][3]

图四-3-2

令这个矩阵为A，Aij表示从i号岛到j号岛是否连通，连通标1，不连通标0，它还有另外一个含义，就是经过1天，从i岛到j岛的方案数，利用矩阵的传递性，

A2的第i行的第j列则表示经过2天，从i岛到j岛的方案数，同样的，An则表示了经过n天，从i岛到j岛的方案数，那么问题就转化成了求AnMOD100000007的值了。

An当n为偶数的时候等于(An/2)*(An/2)；当n为奇数的时候，等于(An/2)*(An/2)*A，这样求解矩阵An就可以在O(logn)的时间内完成了，加法和乘法对MOD操作都是可交换的（即“先加再模”和“先模再加再模”等价），所以可以在矩阵乘法求解的时候，一旦超出模数，就执行取模操作。

最后求得的矩阵T=AnMOD100000007，那么T[1][1]就是我们要求的解了。

4、斜率优化

【例题16】n（n<=500000）个单词，每个单词输出的花费为Ci(1<=i<=n)，将k个连续的单词输出在一行的花费为：

其中M为常数，求一个最佳方案，使得输出所有单词总的花费最小。

令d[i]为前i个单词组织出的最小花费，s[i] = sum{Ck | 0 <= k <= i }，其中s[0] = 0

状态转移方程 d[i] = min{ d[j] + (s[i] - s[j])2 + M | 0 <= j < i }   (1 <= i <= n)

这是个1D/1D问题，空间复杂度O(n), 时间复杂度为O(n2)，对于500000的数据来说是不可能在给定时间出解的。

令g[j] = d[j] + (s[i] - s[j])2+ M，表示由 j 到 i 的决策。

对于两个决策点 j < k，如果k的决策值小于j （即g[k] < g[j]），则有：

       d[k] + (s[i] - s[k]) 2 + M < d[j] + (s[i] - s[j])2+ M，然后将左边转化成关于j和k的表达式，右边转化成只有i的表达式。

 (中间省略t行推导过程...，t >= 5)

       (d[j] - d[k] + s[j]2- s[k]2) / (s[j] - s[k]) < 2*s[i]

令xj = d[j] + s[j]2,   yj = s[j]，则原式转化成： (xj - xk) / (yj - yk) < 2*s[i]

不等式左边是个斜率的形式，我们用斜率函数来表示 slope(j, k) = (xj - xk) / (yj - yk)

那么这里我们可以得出两个结论：

1、当两个决策j、k (j < k)满足 slope(j, k) < 2*s[i]时，j决策是个无用决策，并且因为s[i]是个单调不降的，所以对于i < i'，则有slope(j, k) < 2*s[i] < 2*s[i']，即j决策在随着i增大的过程中也是一直都用不到的。

 2、对于当前需要计算的值f[i]，存在三个决策j、k、l，并且有 j < k < l，如果slope(j, k) > slope(k, l)，则k这个决策是个无用决策，证明需要分情况讨论：

             i. slope(k, l) < 2*s[i]，则l的决策比k更优；

             ii. slope(k, l) >= 2*s[i]，则 slope(j, k) > slope(k, l) >= 2*s[i]，j的决策比k更优；

             综上所述，当slope(j, k) > slope(k, l)时，k是无用决策；

 那么可以用单调队列来维护一个决策队列的单调性，单调队列存的是决策序列。

一开始队列里只有一个决策，就是0这个点（虚拟出的初始决策），根据第一个结论，如果队列里面决策数目大于1，则判断slope( Q[front], Q[front+1] ) < 2*s[i]是否成立，如果成立，Q[front]是个无用决策，front ++，如果不成立那么Q[front]必定是当前i的最优决策，通过状态转移方程计算f[i]的值，然后再根据第二个结论，判断slope(Q[rear-2], Q[rear-1]) > slope(Q[rear-1], i)是否成立，如果成立，那么Q[rear-1]必定是个无用决策，rear --，如果不成立，则将 i 作为当前决策 插入到队列尾， 即 Q[rear++] = i。

这题需要注意，斜率计算的时候，分母有可能为0的情况。

5、树状数组优化

树状数组是一种数据结构，它支持两种操作：

1、对点更新，即在给你(x,v)的情况下，在下标x的位置累加一个和v（耗时O(log(n))）。

函数表示voidadd(x,v);

2、成端求和，给定一段区间[x,y]，求区间内数据的和（这些数据就是第一个操作累加的数据，耗时O(log(n))）。

函数表示intsum(x,y);

用其它数据结构也是可以实现上述操作的，例如线段树（可以认为它是一种轻量级的线段树，但是线段树能解决的问题更加普遍，而树状数组只能处理求和问题），但是树状数组的实现方便、常数复杂度低，使得它在解决对点更新成端求和问题上成为首选。这里并不会讲它的具体实现，有兴趣请参见树状数组。

【例题17】给定一个n(n<=100000)个元素的序列a[i](1<=a[i]<=INF)，定义"和谐序列"为序列的任何两个相邻元素相差不超过K，求a[i]的子序列中，"和谐序列"的个数MOD10000007。

用d[i]表示以第i个元素结尾的"和谐序列"的个数，令d[0]=1，那么sum{d[i]|1<=i<=n}就是我们要求的解。列出状态转移方程：d[i]=sum{d[j]|j==0||j<i&&abs(a[i]-a[j])<=K}

这是一个1D/1D问题，如果不进行任何优化，时间复杂度是O(n^2)。

我们首先假设K是个无限大的数，也就是不考虑abs(a[i]-a[j])<=K这个限制，那这个问题要怎么做？很显然d[1]=1，d[2]=1+d[1]，d[3]=d[1]+d[2]+1（这里的1其实是状态转移方程中j==0的情况，也就是只有一个数a[i]的情况），更加一般地：d[i]=sum{d[j]|j<i}+1对于这一步状态转移还是O(n)的，但是我们可以将它稍加变形，如下：

d[i]=sum(1,INF)+1;(这里的sum是树状数组的区间求和函数)

得到d[i]的值后，再将d[i]插入到树状数组中，利用树状数组第1条操作add(a[i],d[i])；

基于这样的一种思路，我们发现即使有了限制K，同样也是可以求解的，只是在求和的时候进行如下操作：

d[i]=sum(a[i]-K,a[i]+K)+1;

这样就把原本O(n)的状态转移变成了O（logn），整个算法时间复杂度O（logn）。

6、线段树优化

线段树

是一种完全二叉树，它支持区间求和、区间最值等一系列区间问题，这里为了将问题简化，直接给出求值函数而暂时不去讨论它的具体实现，有兴趣的可以自行寻找资料。线段树可以扩展到二维，二维线段树是一棵四叉树，一般用于解决平面统计问题，参见二维线段树。

这里给出线段树的求区间最值需要用到的函数，即：

1、insert(x,v)在下标为x的位置插入一个值v；耗时O(log(n))

2、query(l,r)求下标在[l,r]上的最值；耗时O(log(n))

【例题18】详见例题13

还是以最长单调子序列为例，状态转移方程为：

d[i]=max{d[j]|j<i&&a[j]<a[i]}+1

这里我们首先要保证1<=a[i]<=n，如果a[i]是实数域的话，首先要对a[i]进行离散化，排序后从小到大重新编号，最小的a[i]编号为1，最大的a[i]编号为n。

对于状态转移执行线段树的询问操作：d[i]=query(1,a[i]-1)+1然后再执行插入操作：insert(a[i],d[i])状态转移同样耗时O(logn)。

这个思想和树状数组的思想很像，大体思路都是将数本身映射到某个数据结构的下标。

7、其他优化

a.散列HASH状态表示

b.结合数论优化

c.结合计算几何优化

d.四边形不等式优化

e.等等

五、动态规划题集整理
  1、递推

        Recursion Practice                              ★☆☆☆☆          几个初级递推
        Put Apple                                       ★☆☆☆☆

        Tri Tiling                                      ★☆☆☆☆          【例题1】
        Computer Transformation                         ★☆☆☆☆          【例题2】
        Train Problem II                                ★☆☆☆☆          
        How Many Trees?                                 ★☆☆☆☆          
        Buy the Ticket                                  ★☆☆☆☆          
        Game of Connections                             ★☆☆☆☆
        Count the Trees                                 ★☆☆☆☆
        Circle                                          ★☆☆☆☆
        Combinations, Once Again                        ★★☆☆☆
        Closing Ceremony of Sunny Cup                   ★★☆☆☆           
        Rooted Trees Problem                            ★★☆☆☆          
        Water Treatment Plants                          ★★☆☆☆           
        One Person                                      ★★☆☆☆
        Relax! It’s just a game                        ★★☆☆☆
        N Knight                                        ★★★☆☆
        Connected Graph                                 ★★★★★          楼天城“男人八题”之一

   2、记忆化搜索

        Function Run Fun                                ★☆☆☆☆          【例题3】

        FatMouse and Cheese                             ★☆☆☆☆          经典迷宫问题

        Cheapest Palindrome                             ★★☆☆☆ 

        A Mini Locomotive                               ★★☆☆☆

        Millenium Leapcow                               ★★☆☆☆

        Brackets Sequence                               ★★★☆☆          经典记忆化

        Chessboard Cutting                              ★★★☆☆          《算法艺术和信息学竞赛》例题

        Number Cutting Game                             ★★★☆☆


   3、最长单调子序列

        Constructing Roads In JG Kingdom                ★★☆☆☆

        Stock Exchange                                  ★★☆☆☆

        Wooden Sticks                                   ★★☆☆☆

        Bridging signals                                ★★☆☆☆

        BUY LOW, BUY LOWER                              ★★☆☆☆         要求需要输出方案数

        Longest Ordered Subsequence                     ★★☆☆☆

        Crossed Matchings                               ★★☆☆☆

        Jack's struggle                                 ★★★☆☆          稍微做点转化

   4、最大M子段和

        Max Sum                                         ★☆☆☆☆              最大子段和

        Max Sum Plus Plus                               ★★☆☆☆              最大M子段和

        To The Max                                      ★★☆☆☆              最大子矩阵

        Max Sequence                                    ★★☆☆☆              最大2子段和

        Maximum sum                                     ★★☆☆☆              最大2子段和

        最大连续子序列                                  ★★☆☆☆              最大子段和

        Largest Rectangle in a Histogram                ★★☆☆☆              最大子矩阵变形

        City Game                                       ★★☆☆☆              最大子矩阵扩展

        Matrix Swapping II                              ★★★☆☆              最大子矩阵变形后扩展

   5、线性模型

        Skiing                                          ★☆☆☆☆

        Super Jumping! Jumping! Jumping!                ★☆☆☆☆ 

        Milking Time                                    ★★☆☆☆         区间问题的线性模型

        Computers                                       ★★☆☆☆         【例题5】

        Bridge over a rough river                       ★★★☆☆         【例题6】

        Crossing River                                  ★★★☆☆         【例题6】大数据版

        Blocks                                          ★★★☆☆          

        Parallel Expectations                           ★★★★☆         线性模型黑书案例

       6、区间模型

        Palindrome                                      ★☆☆☆☆         【例题7】

        See Palindrome Again                            ★★★☆☆

       7、背包模型

        饭卡                                            ★☆☆☆☆              01背包

        I NEED A OFFER!                                 ★☆☆☆☆              概率转化

        Bone Collector                                  ★☆☆☆☆              01背包

        最大报销额                                      ★☆☆☆☆              01背包

        Duty Free Shop                                  ★★☆☆☆              01背包

        Robberies                                       ★★☆☆☆              【例题8】 

        Piggy-Bank                                      ★☆☆☆☆              完全背包

        Cash Machine                                    ★☆☆☆☆              多重背包

        Coins                                           ★★☆☆☆              多重背包，楼天城“男人八题”之一

        I love sneakers!                                ★★★☆☆              背包变形

       8、状态压缩模型

        ChessboardProblem                               ★☆☆☆☆              比较基础的状态压缩

        Number of Locks                                 ★☆☆☆☆              简单状态压缩问题

        Islands and Bridges                             ★★☆☆☆              【例题9】

        Tiling a Grid With Dominoes                     ★★☆☆☆              骨牌铺方格 4XN的情况

        Mondriaan's Dream                               ★★☆☆☆              【例题10】的简易版

        Renovation Problem                              ★★☆☆☆              简单摆放问题

        The Number of set                               ★★☆☆☆

        Hardwood floor                                  ★★★☆☆              【例题10】二进制状态压缩鼻祖

        Tetris Comes Back                               ★★★☆☆              纸老虎题

        Bugs Integrated, Inc.                           ★★★☆☆              三进制状态压缩鼻祖

        Another Chocolate Maniac                        ★★★☆☆              三进制

        Emplacement                                     ★★★☆☆              类似Bugs那题，三进制

        Toy bricks                                      ★★★☆☆              四进制， 左移运算高于&

        Quad Tiling                                     ★★★☆☆              骨牌铺方格 4XN的情况 利用矩阵优化

        Eat the Trees                                   ★★★☆☆              插头DP入门题

        Formula 1                                       ★★★☆☆              插头DP入门题

        The Hive II                                     ★★★☆☆              插头DP

        Plan                                            ★★★☆☆              插头DP

        Manhattan Wiring                                ★★★☆☆              插头DP

        Pandora adventure                               ★★★★☆              插头DP

        Tony's Tour                                     ★★★★☆              插头DP，楼天城“男人八题”之一

        Pipes                                           ★★★★☆              插头DP

        circuits                                        ★★★★☆              插头DP

        Beautiful Meadow                                ★★★★☆              插头DP

        I-country                                       ★★★★☆              高维状态表示

        Permutaion                                      ★★★★☆              牛逼的状态表示

        01-K Code                                       ★★★★☆

        Tour in the Castle                              ★★★★★              插头DP（难）

        The Floor Bricks                                ★★★★★              四进制（需要优化）

       9、树状模型

        Anniversary party                               ★☆☆☆☆              树形DP入门

        Strategic game                                  ★☆☆☆☆              树形DP入门

        Computer                                        ★★☆☆☆ 

        Long Live the Queen                             ★★☆☆☆

        最优连通子集                                    ★★☆☆☆ 

        Computer Network                                ★★☆☆☆

        Rebuilding Roads                                ★★★☆☆              树形DP+背包

        New Year Bonus Grant                            ★★★☆☆

        How Many Paths Are There                        ★★★☆☆  

        Intermediate Rounds for Multicast               ★★★★☆

        Fire                                            ★★★★☆

        Walking Race                                    ★★★★☆

        Tree                                            ★★★★★              树形DP，楼天城“男人八题”之一

           10、滚动数组优化常见问题

        Palindrome                                      ★☆☆☆☆

        Telephone Wire                                  ★☆☆☆☆

        Gangsters                                       ★☆☆☆☆

        Dominoes                                        ★☆☆☆☆

        Cow Exhibition                                  ★☆☆☆☆

        Supermarket                                     ★★☆☆☆
 

        11、决策单调性

        Print Article                                   ★★★☆☆

        Lawrence                                        ★★★☆☆

        Batch Scheduling                                ★★★☆☆

        K-Anonymous Sequence                            ★★★☆☆

        Cut the Sequence                                ★★★☆☆

        12、常用优化

        Divisibility                                    ★★☆☆☆        利用同余性质

        Magic Multiplying Machine                       ★★☆☆☆        利用同余性质

        Moving Computer                                 ★★☆☆☆        散列HASH表示状态

        Post Office                                     ★★★☆☆        四边形不等式

        Minimizing maximizer                            ★★★☆☆        线段树优化

        Man Down                                        ★★★☆☆        线段树优化

        So you want to be a 2n-aire?                    ★★★☆☆        期望问题

        Expected Allowance                              ★★★☆☆        期望问题

        Greatest Common Increase Subseq                 ★★★☆☆        二维线段树优化

        Traversal                                       ★★★☆☆        树状数组优化

        Find the nondecreasing subsequences             ★★★☆☆        树状数组优化

        Not Too Convex Hull                             ★★★★☆        利用凸包进行状态转移

        In Action                                       ★★★☆☆        最短路+背包

        Search of Concatenated Strings                  ★★★☆☆        STL bitset 应用

        13、其他类型的动态规划

        Common Subsequence                              2D/0D

        Advanced Fruits                                 2D/0D

        Travel                                          2D/1D

        RIPOFF                                          2D/1D

        Balls                                           2D/1D

        Projects                                        2D/1D

        Cow Roller Coaster                              2D/1D 

        LITTLE SHOP OF FLOWERS                          2D/1D

        Pearls                                          2D/1D

        Spiderman                                       2D/0D

        The Triangle                        2D/0D 

        Triangles                           2D/0D

        Magazine Delivery                     3D/0D

        Tourist                             3D/0D

        Rectangle                           2D/1D

        Message                             2D/1D

        Bigger is Better                      2D/1D

        Girl Friend II                       2D/1D

        Phalanx                             2D/1D

        Spiderman                           最坏复杂度O(NK)，K最大为1000000，呵呵

        Find a path                                     3D/1D 公式简化，N维不能解决的问题试着用N+1维来求解