本文转自公众号 数学与算法之美

五个囚犯先后从 100 颗绿豆中抓绿豆。抓得最多和最少的人将被处死，不能交流，可以摸出剩下绿豆的数量，谁的存活几率最大？

提示：

1.他们都是很聪明的人；

2.他们的原则是先求保命，再去多杀人；

3.100 颗不必都分完，但要保证每人至少抓一颗；

4.若有重复的情况，则也算最大和最小，一并处死。

这道题怎么做，取决于我们如何从数学的角度理解题干中这句话：

「他们的原则是先求保命，再去多杀人」。

 我的理解是： 

1. 每个人采取方案，使得剩下的人在采取最佳方案的时候，自己的存活概率最大；

2. 如果有多种方案使得自己的存活概率最大且相同，则采取杀死人最多的方案。

假设我的理解正确，那么，这道题将会有一个可怕的答案。

定义：m_n为第n 个人取走的绿豆数，而M_n为前n个人取走的总绿豆数

 引理 1：

当 n个人 (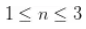) 取过绿豆时，如果被取走的绿豆数满足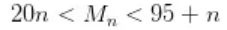

则第n+1个人应该取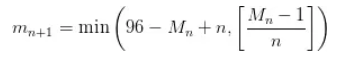颗绿豆；

 证明： 

这个方案，可以确保自己不死，同时剩下未取豆子的人死亡概率最大。

其中：

 96-M_n +n是确保剩下的人至少有一颗绿豆可选，且自己至少取了 2 颗；

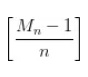是确保自己取的绿豆数至少比前面取的最多的人少 1 ；

由于 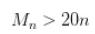, 有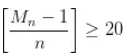, 这不仅保证了自己取的豆子数不是最多的，并且其他人不可能都取到那么多，所以自己必然存活；

如果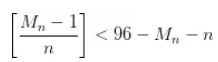，他在确保自己存活的情况下，使得剩下的豆子数最少，这样可以杀更多的人；

如果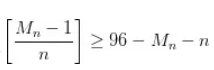，他在确保自己存活的情况下，剩下的人每个人只能取 1 颗豆子，确保杀死剩下的所有人；

 推论 1：如果第 1 个人想要存活，那么他取的豆子数不能超过 20 颗，否则，后面的人只要采取引理 1 的方案，将保证自己存活，且此时第 1 个人会因为取的绿豆数最多而死亡，而最后 1~3 个人（根据第 1 个人取的绿豆数）会因为自己取的豆子数最少而死亡；

 引理 2：当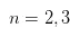时，若，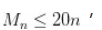

则第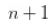 个人应该取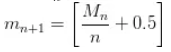 颗绿豆来确保自己的存活概率最高，其中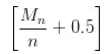，是均值的四舍五入）

因为当且仅当在这种情况下，只要前面的人取的绿豆数的最大最小值之差不小于 2，自己就确保能存活（否则存活范围会变窄）

对于第 5 个人，这个条件可能不成立，比如见到前面四个人取了 62 颗，可能是 14+16+16+16，也可能是 15+15+15+17，所以他无论取 15 颗还是 16 颗都有机会但不能确保自己存活。

而所有人取绿豆的最大最小值的差不大于 1，所有人都得死；

引理 3：当大家都极度自私的情况下，前 2 个人没有存活的可能

这是因为由引理 2，如果第 3~5 个人都会采取对他们而言存活概率的方案，如果第 2 个人和第 1 个人取的绿豆数差超过 1 个，那前两个人就包揽了最大最小值，必须死，如果差不超过 1，则所有人都得死；

既然第 1 个人没有存活概率，那他的目标就很耐人寻味了：

如果自己没有存活概率——

    选择 1：杀死尽可能多的人

    选择 2：尽可能拯救更多的人

按照我的假设，应该是前者。

既然第 1 个人没有存活概率，不妨让大家都死得干净些——取走 96 颗绿豆！

但如果，第 1 个人有点恻隐之心，做出了选择 2：

那，他会取走 21~33 的豆子数，根据引理 1，第 2~4 个人会存活；

所以，本题根据对题意的不同理解，有两解：

    所有人都死亡；

    第 2~4 个人存活；

而对于第 1 个囚犯，他将面临一个哲学难题：

如果自己不可能活下去，你会选择让别人陪葬，还是让其他人好好活下去？

如果是你，会怎么选择呢？

数学妙啊！妙！

这个是不要要归于博弈论的范畴？

记得还有个著名的海盗分金~~