本文转自 handpub 有增删
1. 引言
t分布是统计学中的一类重要分布,英国统计学家哥塞特(Gosset)发现了它与标准正态分布的微小差别,在置信区间估计和显著性检验问题的计算中起到了重要作用。从各种有关统计资料中可以发现很多有关t分布的应用,例如在渔业中、农业、工业等中的应用,为此可用t分布进行区间估计和假设检验来解决一些实际生活问题。
t检验是假设检验方法最常用方法之一,常用于正态总体均值的假设检验。单边检验和双边检验的拒绝域在许多统计学和概率论的教材中都给出了明确的定义。当样本数据比较多的时候,t检验方法虽然简单,但其计算量仍然比较大,因此我们可以使用SPSS软件来实现t检验。本文用SPSS13.0分别讨论了单样本与独立两样本两种情形的t检验。
2. t分布
2.1. t分布的定义
假设随机变量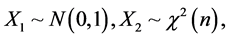 且变量
且变量 与变量
与变量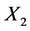 相互独立,则称
相互独立,则称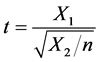 的分布为自由度为n的t分布,记作
的分布为自由度为n的t分布,记作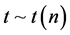 。
。
下面导出t分布的密度函数。由标准正态密度函数的对称性可知,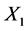 与
与 相同分布相同,从而t与−t有相同分布。这说明:对任意实数y有
相同分布相同,从而t与−t有相同分布。这说明:对任意实数y有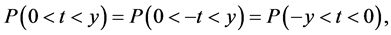
于是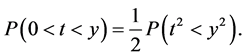
由F变量构造可知,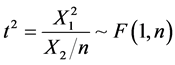 ,将上式两边关于y求导可得t分布的密度函数为
,将上式两边关于y求导可得t分布的密度函数为

这就是自由度为n的t分布的密度函数。
t分布是一簇曲线,其形态大小变化与自由度的大小相关。如果自由度v越小,t分布的曲线就越低平;如果v自由度越大,t分布的曲线越与标准正态分布曲线接近,t分布图像,如图1。
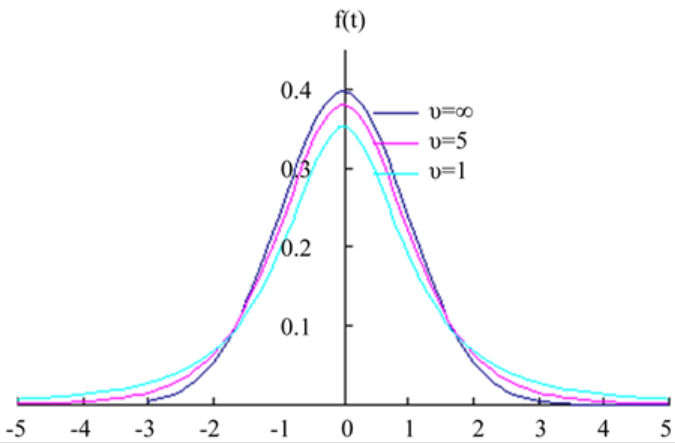
图1. 自由度为1、5、∞的t分布
2.2. t分布的性质
性质1:设 是来自正态分布
是来自正态分布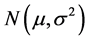 的一个样本,
的一个样本,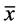 与
与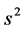 分别是该样本均值与样本方差,则有
分别是该样本均值与样本方差,则有
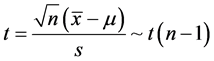 (1.1)
(1.1)
证明:由于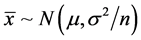 所以可以推出
所以可以推出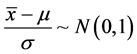 。将(1.1)式左端改写成为
。将(1.1)式左端改写成为
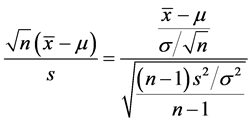
因为分母的根号里是自由度为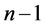 的
的 变量除以它的自由度,分子是标准正态变量,并且分子与分母相互独立,我们由t分布定义可知
变量除以它的自由度,分子是标准正态变量,并且分子与分母相互独立,我们由t分布定义可知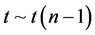 ,证毕。
,证毕。
性质2:设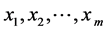 是来自
是来自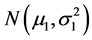 的样本,
的样本,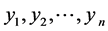 是来自
是来自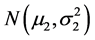 的样本,且此两样本相互独立,记
的样本,且此两样本相互独立,记
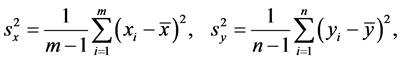
其中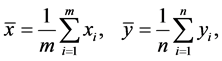
则有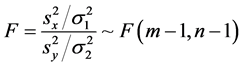
设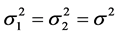 ,并记
,并记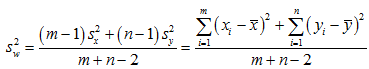
则有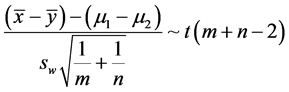
3. t分布在区间估计中应用
3.1. 单样本的区间估计
3.1.1. 均值的区间估计
方差未知时,t统计量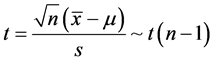 ,其中s为样本标准差
,其中s为样本标准差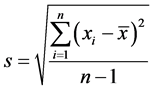 ,n为样本容量.
,n为样本容量.
利用t分布,对于任意可能的偏差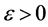 ,我们计算概率
,我们计算概率 , 设
, 设
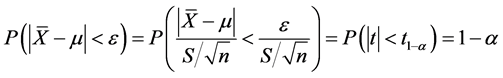 其中
其中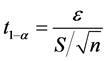 ,即
,即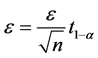 ,则对于置信度
,则对于置信度
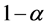 ,可以查t分布表(自由度为
,可以查t分布表(自由度为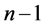 ),求出
),求出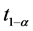 ,进而按上式求出偏差
,进而按上式求出偏差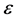 ,便可得到
,便可得到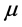 的置信区间为
的置信区间为
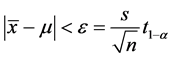 ,或
,或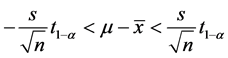 ,
,
即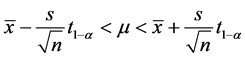 。
。
也常记为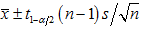 ,此处
,此处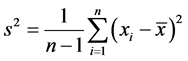 是
是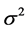 的无偏估计。
的无偏估计。
3.1.2. 单样本区间估计的应用
1) 在渔业中的应用
例2.1 某水产研究所池塘养殖室,1979年在某渔场一块面积15亩的池塘,他们将利用城市的污水进行养殖鲢、鳙鱼来进行试验,年初时鲢、鳙鱼种在池塘中各放入12,000条(其中鱼的个体长约8寸),经数据统计知年终取样捕捞鳙鱼22条,经计算可以得到样本均值为 市斤,该样本的标准差为
市斤,该样本的标准差为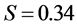 市斤.试求该样本总体均值
市斤.试求该样本总体均值 以90%的置信区间。
以90%的置信区间。
解:自由度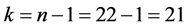 和
和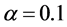 查t分布表可得到
查t分布表可得到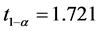 ,由此可得偏差为
,由此可得偏差为
所以置信区间为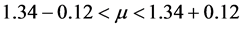
即 。
。
也就是说,我们有90%的把握推断该鱼塘鳙鱼平均体重为1.22~1.46市斤.有时候我们需要知道样本量,故可通过单样本区间估计得出样本量。样本量的确定,从2.1.1的推导我们可以知道,对于置信区间 ,偏差
,偏差 满足
满足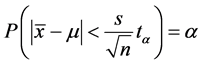 。由
。由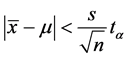 可以得到
可以得到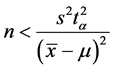 通常我们取
通常我们取 等于自由度为
等于自由度为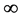 时的值来确定取样数比较可靠:
时的值来确定取样数比较可靠: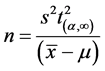 ,其中
,其中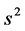 可以在正式调查前的预备调查中的实际算出。
可以在正式调查前的预备调查中的实际算出。
例2.2 在上例所述的池塘中,假设已知鲢鱼样本标准差为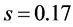 市斤,如果我们要求样本均值与总体均值的允许偏差为总体均值的允许偏差为0.07市斤,试求90%置信概率的鲢鱼样本应取样数。
市斤,如果我们要求样本均值与总体均值的允许偏差为总体均值的允许偏差为0.07市斤,试求90%置信概率的鲢鱼样本应取样数。
解: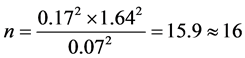
即取样数为16即可。
2) 单样本区间估计在产品寿命中的应用
例:假定某种轮胎的寿命服从正态分布.为了估计这种轮胎的平均使用寿命,我们随机地抽取12只轮胎进行试用,测得它们的使用寿命(单位:万千米)如表1。

表1. 随机抽取12只轮胎的使用寿命(单位:万千米)
试求平均寿命的0.95置信区间。
解:这里正态总体的标准差未知,故可使用t分布求均值的置信区间.其中 ,
,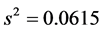 .取
.取 ,查t分布表可知
,查t分布表可知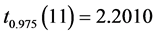 ,故轮胎平均寿命的0.95置信区间为
,故轮胎平均寿命的0.95置信区间为
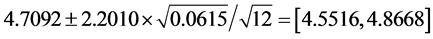
实际应用当中,我们总期望轮胎的使用寿命能够越长越好,所以,这里我们可以只求轮胎平均寿命的置信下限,即构造单侧的置信下限,由于
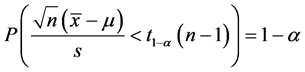
从上述不等式变形可以得到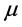 的
的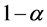 置信下限为
置信下限为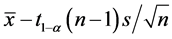 。将
。将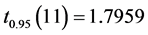 代入计算可得轮胎平均寿命
代入计算可得轮胎平均寿命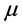 的0.95置信下限为4.5806(万千米)。
的0.95置信下限为4.5806(万千米)。
例2.4 [2] 假设某种灯泡的寿命服从正态分布,我们先从一批灯泡中随机抽取16只灯泡,测得这16只灯泡使用寿命(小时)如表2。

表2. 随机抽取16只灯泡的使用寿命
试确定该批灯泡平均使用寿命95%的置信区间。
解:根据抽样结果计算的:
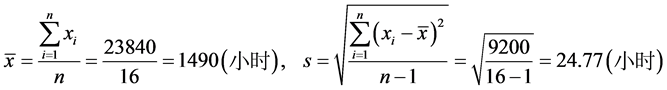
根据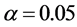 查t分布表得
查t分布表得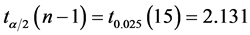 ,故平均使用寿命的置信区间为:
,故平均使用寿命的置信区间为:
故该种灯泡平均使用寿命95%的置信区间为(1476.8,1503.2)小时。
3.2. 独立两样本的区间估计
设 是来自
是来自 的样本,
的样本,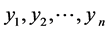 是来自
是来自 的样本,且此两样本相互独立。
的样本,且此两样本相互独立。 与
与 分别是它们的样本均值,记
分别是它们的样本均值,记
 ,
, ,
,
分别为样本x和样本y的样本方差,下面讨论两个均值差。
3.2.1. 两样本均值差的区间估计
1) 两样本方差相等且未知时,枢轴量 ,
,
记 ,则
,则 的置信区间为
的置信区间为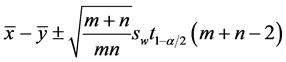
2) 已知两样本方差比值时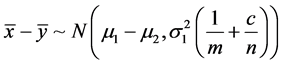 。
。
 ,
,
枢轴量 ,
,
则 的
的 置信区间为
置信区间为 。
。
3.2.2. 独立两样本的区间估计的应用
1) 在军事中的应用
例:为了比较某两种型号为a,b的两种步枪子弹的枪口速度,随机地抽取出a型子弹10发,得到枪口速度的平均值为 ,标准差
,标准差 ,随机地抽取出b型子弹20发,得到枪口速度的平均值为
,随机地抽取出b型子弹20发,得到枪口速度的平均值为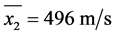 .标准差
.标准差 .这里我们都假设两样本都可认为近似的服从正态分布,且两种型号子弹的生产过程可认为方差相等,求两样本均值差
.这里我们都假设两样本都可认为近似的服从正态分布,且两种型号子弹的生产过程可认为方差相等,求两样本均值差 的一个置信水平为0.95的置信区间。
的一个置信水平为0.95的置信区间。
解:我们可以知道两个总体的样本是相互独立的,且假设两样本的方差相等,但方差的数值未知,
所以可以利用公式 来求均值的置信区间,由于
来求均值的置信区间,由于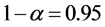 ,
, ,
,
 ,
, ,
, ,
, 。
。 ,
, ,故所求的两总体均值差
,故所求的两总体均值差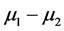 的一个置信水平0.95的置信区间是
的一个置信水平0.95的置信区间是 ,即
,即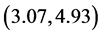 。
。
2) 独立两样本的区间估计在工业中的应用
例2.6为了提升某一化学生产过程的得率,我们么试图采用一种新的催化剂。为了慎重起见,需要在实验工厂对此新的催化剂进行实验.假设采用原来的催化剂进行了 次试验,我们得到的得率的平均值
次试验,我们得到的得率的平均值 ,其样本方差为
,其样本方差为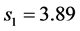 ;又采用新的催化剂进行了
;又采用新的催化剂进行了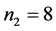 次试验,得到得率的平均值
次试验,得到得率的平均值 ,样本方差
,样本方差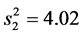 .这里假设两样本都可认为服从正态分布,两样本相互独立,并且两样本的方差相等。试求两样本总体均值差
.这里假设两样本都可认为服从正态分布,两样本相互独立,并且两样本的方差相等。试求两样本总体均值差 的置信水平为0.95的置信区间。
的置信水平为0.95的置信区间。
解: ,
, ,由公式
,由公式
求得置信区间为 ,即
,即 。
。
因为得到的置信区间包含零,在实际应用当中我们认为采用这两种催化剂所得的得率的均值是没有显著差别。
4. t分布在假设检验中的应用
4.1. 单样本t检验
4.1.1. 单样本t检验定义
t检验是常用的假设检验方法之一,常用于正态总体均值的假设检验,单样本t检验中
当 (1)
(1)
的假设检验问题成为双边假设检验;
当 (2)
(2)
的假设检验问题成为左边检验
当 (3)
(3)
的假设检验问题成为右边检验
在单个正态总体 均值
均值 的检验中,当
的检验中,当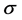 未知时,可选用t检验中(1)、(2)、(3)。
未知时,可选用t检验中(1)、(2)、(3)。 未知时,
未知时, 是
是 的一个置信水平为
的一个置信水平为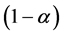 的单侧置信区间,其中
的单侧置信区间,其中 是置信下限,即对于任意的
是置信下限,即对于任意的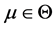 ,
,
有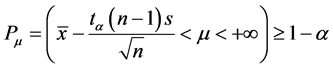 . (4)
. (4)
考虑右边检验 ,其拒绝为
,其拒绝为 ,等价于
,等价于 , (5)
, (5)
恒等变形得 ,即
,即 ;同理如果
;同理如果 ,则
,则 ,恒等变形得
,恒等变形得
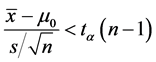 (6)
(6)
即有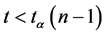 ,此时应接受
,此时应接受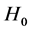 .所以我们要检验假设(3),可先求出
.所以我们要检验假设(3),可先求出 的置信水平为
的置信水平为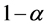 的单
的单
侧置信区间 ,然后考察区间是否包含
,然后考察区间是否包含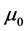 ,
,
若 ,则接受
,则接受 ;若
;若 ,则拒绝
,则拒绝 。
。
4.1.2. 单样本t检验的应用
1) 单样本t检验在产品寿命中的应用
单样本在SPSS统计软件中,置信区间类型为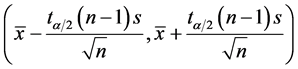 (置信度为
(置信度为 ),故我们通过求出
),故我们通过求出 的置信度为
的置信度为 的置信区间
的置信区间 ,即可求出
,即可求出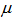 的置信度为
的置信度为 的单侧置信区间
的单侧置信区间 ,同理按上述方法可以检验假设(3)。
,同理按上述方法可以检验假设(3)。
例 某种产品的使用寿命x(以h计)服从正态分布 ,
, 未知,随机抽取16只该产品,测得16只该产品的使用寿命如表3。
未知,随机抽取16只该产品,测得16只该产品的使用寿命如表3。

表3. 测得16只产品的使用寿命(单位:h)
问是否可以认为该产品的平均使用寿命大于225小时(取显著性水平为 )?
)?
解:原假设和备择假设为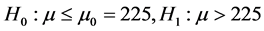 ,建立数据文件,然后点击软件SPSS13.0中“Analyze → Descriptive Statistics → Explore” [5] -[10] 就能得出图2的结果,其中置信度设置为
,建立数据文件,然后点击软件SPSS13.0中“Analyze → Descriptive Statistics → Explore” [5] -[10] 就能得出图2的结果,其中置信度设置为 。
。
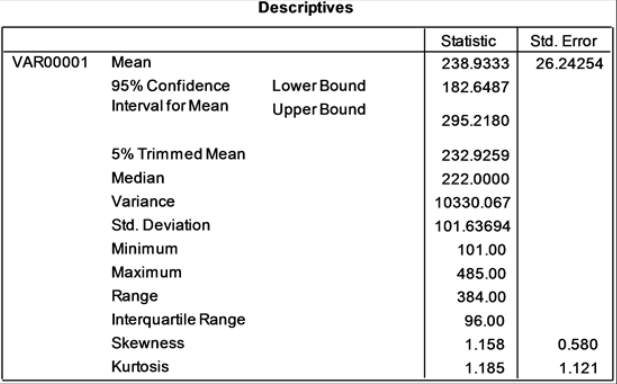
图2. 某种产品抽样样本数据表
由图2可知,均值 的置信度为
的置信度为 的单侧置信区间为
的单侧置信区间为 。又因为
。又因为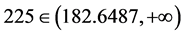 ,所以在显著性水平
,所以在显著性水平 下接受
下接受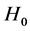 ,故认为该产品的平均使用寿命小于等于225小时。
,故认为该产品的平均使用寿命小于等于225小时。
2) 单样本t检验在农业中的应用
例3.2 有一种新型农药防治柑桔红蜘蛛,进行了9个校区的实验,其防治效果为:95%,92%,88%,92%,93%,95%,89%,98%,92%,与原用农药的防治效果90%比较,分析其效果是否高于原用农药。
解:在这里应用spss13.0软件来分析,在数据编辑窗口输入分析数据,在软件spss13.0主菜单中选中“Analyze→Compare Means→One-Sample T Test”,打开单一样本T检验主对话框,从左边的变量列表中选中“防治效果”变量之后,点击中部的右拉按钮,使得这个变量就进入到检验分析“Test Variable(s):”框里,用户可以从左边变量列表里选择一个或多个变量进行分析。在“Test Variable(s)”输入栏里,输入用于比较检验的均值:在本例中为90。单击“Options”按钮,打开设置检验的置信度和缺失值对话框。在“Confidence Interval:”框输入置信度水平,系统默认为95%。在“Missing Values”栏里选择缺失值处理方式:输入完成后,在过程主窗口中单击“OK”按钮,SPSS输出分析结果如图3。
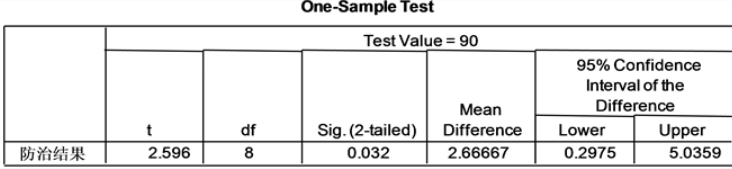
图3. 新旧农药防治效果的t检验结果
从图3中读取数值,t值为2.596,Sig.(2-tailed)为单边t检验的显著性概率0.032,小于0.05,由此得出结论:新型农药和原用农药差异显著。
3) 单样本t检验在材料中的应用
例3.3 某种汽车配件的平均长度要求为12 cm,高于或低于标准均被认为是不合格的。汽车生产企业在购进配件时,通常是经过招标,然后对中标的配件提供的样品进行检验,用来决定是否购进此汽车配件.现在对一个配件提供商提供的10个样本进行了检验。结果如表4。

表4. 10个配件的长度(单位:cm)
假设该供货商生产的配件长度服从正态分布,在0.05的显著性水平下,检验该供货商提供的配件长度符合标准要求?
解:依题意建立如下原假设与备择假设:
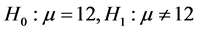
根据样本数据计算得:
由于 为小样本,采用t检验:
为小样本,采用t检验:
根据自由度 ,查t分布表得:
,查t分布表得: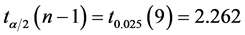 ,
,
由于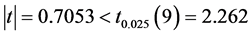 ,所以不拒绝原假设,样本提供的证据还不足以推翻原假设。
,所以不拒绝原假设,样本提供的证据还不足以推翻原假设。
单样本t检验在日化产品中的应用
例3.4,某日化生产厂家生产一批次牙膏,要求牙膏总重为151.70 g,管长15.65 cm。随机抽取该批次30支牙膏,分别称重(g)为(表5)。
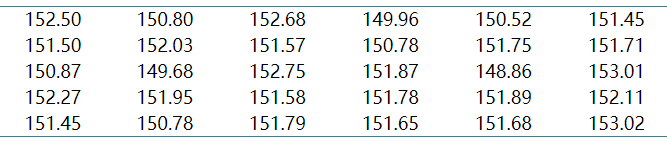
表5. 30支牙膏的称重(单位:g)
灌装后管长(mm)为(表6)。
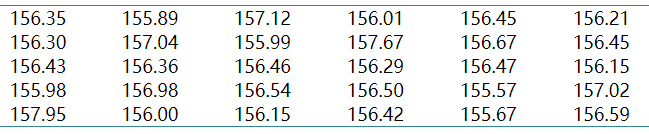
表6. 30支牙膏灌装后管长(单位:mm)
判断这批牙膏是否符合标准要求?
解:应用spss13.0软件来分析,在数据编辑窗口输入分析数据,在软件spss13.0主菜单中选中“Analyze → Compare Means → One-Sample T Test”,打开单一样本T检验主对话框,从左边的变量列表中选中“重量”变量之后,点击中部的右拉按钮,使得这个变量就进入到检验分析“Test Variable(s):”框里。在“Test Variable(s)”输入栏里,输入用于比较检验值:在本例中重量检验值为为151.70,灌装后管长检验值为156.5。单击“Options”按钮,打开设置检验的置信度和缺失值对话框。在“Confidence Interval:”框输入置信度水平,系统默认为95%。在“Missing Values”栏里选择缺失值处理方式:输入完成后,在过程主窗口中单击“OK”按钮,SPSS输出分析结果如图4。
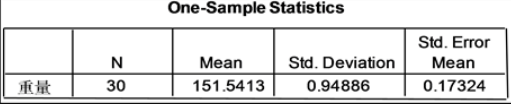
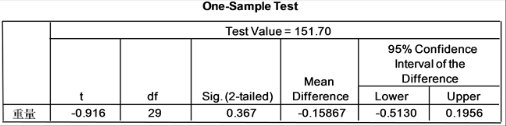
图4. 牙膏灌装重量t检验结果
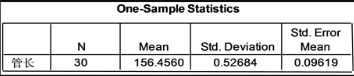
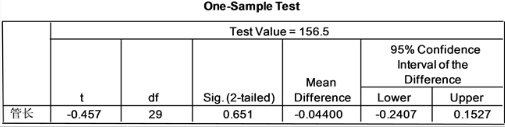
图5. 牙膏灌装管长t检验结果
从图4中可知经单样本双侧t检验得到的显著性水平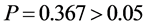 ,故与检验值151.70没有显著性差异,这批牙膏的重量是符合质量要求。
,故与检验值151.70没有显著性差异,这批牙膏的重量是符合质量要求。
从图5中可知经单样本双侧t检验得到的显著性水平 ,故与检验值156.50没有显著性差异,这批牙膏灌装后的管长符合质量要求。
,故与检验值156.50没有显著性差异,这批牙膏灌装后的管长符合质量要求。
对于牙膏来说重量明显大于或小于标准值,通常需要进行设备调整,重量太大,会增加相对的损耗,也容易在灌装过程中造成牙膏软管破损;重量太轻,就会损害消费者的权益。故t检验在牙膏质量检测中起着非常重要的作用。
4.2. 独立两样本t检验
4.2.1 . 独立两样本t检验定义
独立两样本t检验可用于两正态总体均值差的建设检验,设 是来自正态总体
是来自正态总体 的样本,
的样本, 是来自正态总体
是来自正态总体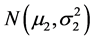 的样本,
的样本, 均未知.两样本相互独立,即他们的样本均值分别为
均未知.两样本相互独立,即他们的样本均值分别为 和
和 ,样本方差为
,样本方差为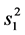 和
和 ,考虑检验问题:
,考虑检验问题:
 ,(7)
,(7)
1.当 时,选用检验统计量
时,选用检验统计量 ,
,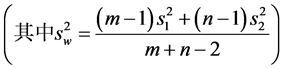 ;
;
2.当 ,用校正的t检验,此时
,用校正的t检验,此时
 , (8)
, (8)
其自由度n计算如下 .
.
与单边单样本t检验类似,在单边独立两样本t检验(7)中,也可先求出量总体均值差 的置信度为
的置信度为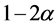 置信区间,从而可以求出
置信区间,从而可以求出 的置信度为
的置信度为 单侧置信区间,再根据
单侧置信区间,再根据 是否属于单侧置信区间,则接受
是否属于单侧置信区间,则接受 ;否则拒绝
;否则拒绝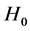 。
。
4.2.2 . 独立两样本t检验的应用
1) 独立两样本t检验在啤酒业中的应用
例在20世纪70年代后期,在酿造啤酒的时候人们发现麦芽的干燥过程中容易形成对人体有伤害的致癌物质亚硝酸二甲胺(NDMA)。到了20世纪80年代初期为了避免酿造啤酒时麦芽干燥过程产生致癌物质亚硝酸二甲胺,研发了一种新型的麦芽干燥过程.下面给出了新老两种麦芽在干燥过程中形成的亚硝酸二甲胺含量(以下数据以20亿份中的份数统计得到):
假设该两样本分服从自正态总体分布,单参数均未知,且该两样本相互独立,分别以 记对应于老、新过程两样本的总体均值、试检验假设
记对应于老、新过程两样本的总体均值、试检验假设

首先将新老两种麦芽在干燥过程中形成的亚硝酸二甲胺含量(表7)数据输入到SPSS13.0中,点击“Analyze→Compare Means→Independent-Samples T test ”,设置好其中的检验变量和分组变量,在选项中设置其置信度为 ,再点击“Continue→OK”,得到图6,图7的分析结果。
,再点击“Continue→OK”,得到图6,图7的分析结果。
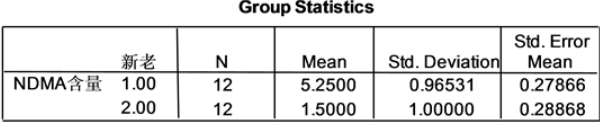
图6. 新老干燥过程中形成的亚硝酸二甲胺含量的统计量结果
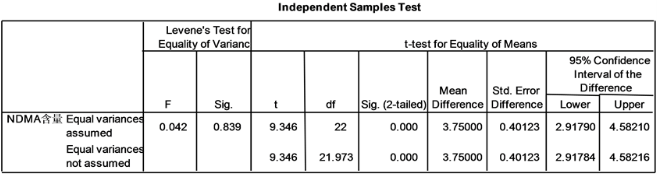
图7. 新老两种麦芽干燥过程中形成的亚硝酸二甲胺含量的t检验结果
从图6中可知, ,故可以认为新、老干燥过程的资料的方差齐,其中两样本均值差
,故可以认为新、老干燥过程的资料的方差齐,其中两样本均值差 的90%的置信区间为
的90%的置信区间为 ,因此
,因此 ,是两样本均值差
,是两样本均值差 的95%的单侧置信区间,由于
的95%的单侧置信区间,由于 ,故在显著性水平
,故在显著性水平 下拒绝
下拒绝 ,即可认为老、新干燥过程的均值差大于2。
,即可认为老、新干燥过程的均值差大于2。
2) 独立两样本t检验在农业中的应用
例3.6 [2] 在某个有小麦丛矮病的麦田里,调查了13株病株和11株健株的植株高度,分析健株高度是否比病株高。其调查数据如表8。

表8. 11株健株和13株病株的植株高度
解:应用SPSS分析,在SPSS中输入数据,在数据编辑窗口输入首先将上述数据输入到SPSS中,点击“Analyze”中的Compare Means并点击Independent-Samples T test,设置好检验变量和分组变量,在
选项中设置置信度水平,设置为95%的置信度水平,输入完成,在过程主窗口中单击“OK”按钮,SPSS输出分析结果如下图8,图9。
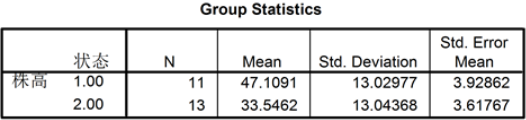
图8. 健株病株高度的统计量结果
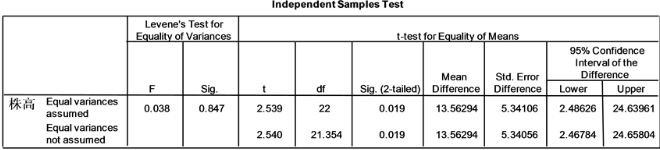
图9. 健株病株高度的t检验结果
分析:从图9可知t的值是2.539,sig.(2-tailed)是双边t检验的显著性概率为0.019,小于0.05,可以得出结论:健株与病株的株高差异显著。
3) 独立两样本t检验在工业的应用
例3.7 [4] 某工厂铸造车间为了提高铸件的耐磨性,制造了一种镍合金铸件用来代铜合金铸件,从两种铸件中分别抽取一个容量分别为8和9的样本,分别测得其硬度(一种耐磨性指标)为(表9)。
根据专业经验,硬度服从正态分布,且方差保持不变,试在显著性水平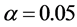 下判断镍合金的硬度是否有明显提高。
下判断镍合金的硬度是否有明显提高。
解:用X表示镍合金的硬度,Y表示铜合金的硬度,则有假设定, ,要检验的假设是
,要检验的假设是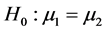 vs
vs .由于两者方差未知但相等,所以采用两样本t检验,经计算,
.由于两者方差未知但相等,所以采用两样本t检验,经计算, ,
,

从而 ,
, ,
,
查表知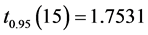 ,由于
,由于 ,故拒绝原假设,可判断镍合金硬度有显著提高。
,故拒绝原假设,可判断镍合金硬度有显著提高。
应用SPSS分析,得出图10和图11:
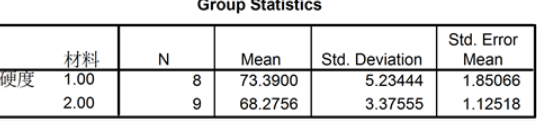
图10. 镍合金硬度的统计量结果
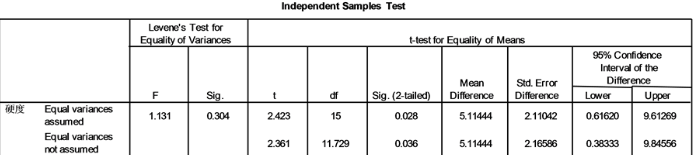
图11. 镍合金硬度的t检验结果
由图11可知t的值是2.423,sig.(2-tailed)是双边t检验的显著性概率为0.028,小于0.05,故也可判断镍合金硬度有显著提高。
例:甲、乙两台机床同时加工某种同类型的零件,已知两台机床加工的零件直径(单位:cm)分别服从正态分布 ,并且有
,并且有 ,为比较两台机床的加工精度有无显著差异,分别独立抽取了甲机床加工的8个零件和乙机床加工的7个零件,通过测量得到两台机床加工零件的样本直径数据如表10:
,为比较两台机床的加工精度有无显著差异,分别独立抽取了甲机床加工的8个零件和乙机床加工的7个零件,通过测量得到两台机床加工零件的样本直径数据如表10:

表10. 两台机床加工零件的样本直径数据(单位:cm)
在 的显著性水平下,样本数据是否提供证据支持“两台机床加工的零件直径不一致”的看法?
的显著性水平下,样本数据是否提供证据支持“两台机床加工的零件直径不一致”的看法?
解:提出的原假设和备择假设为:
两个独立样本的容量都小于30,两个总体方差未知但相等,根据样本数据计算得:
总体方差的合并估计量为:
计算的检验的统计量为:
根据自由度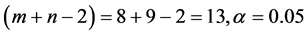 对应的t分布临界值分别是2.160,−2.160检验统计量的值没有落入拒绝域.一次不拒绝原假设.故在0.05的显著性水平下,没有理由认为甲,乙两台机床加工的零件直径不一致。
对应的t分布临界值分别是2.160,−2.160检验统计量的值没有落入拒绝域.一次不拒绝原假设.故在0.05的显著性水平下,没有理由认为甲,乙两台机床加工的零件直径不一致。
应用SPSS分析,得出图12和图13。
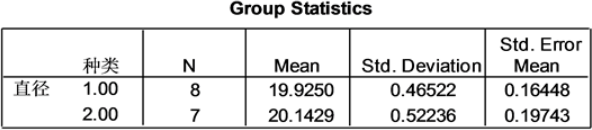
图12. 甲、乙两台机床加工的零件直径的统计量结果
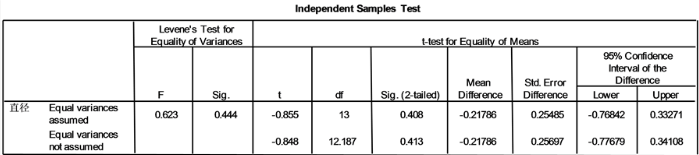
图13. 甲、乙两台机床加工的零件直径的t检验结果
由图13可知t的值是−0.855,sig.(2-tailed)是双边t检验的显著性概率为0.408,大于0.05,故没有理由认为甲,乙两台机床加工的零件直径不一致。
5. t分布和正态分布的区别
1、标准从正态分布与t分布密度函数的比较来看。t分布的的密度函数相比标准正态分布表现为厚尾,随着自由度的逐渐增大,t分布密度函数逐渐接近标准正态分布,当自由度趋于无穷大时,t分布的密度函数趋近于标准正态分布密度函数。下图是用R软件画的标准正态分布(红色)和t(2)(黄色),t(3)(蓝色),t(5)(绿色)的密度函数图,可以看出,随着自由度的增大,t分布的密度函数逐渐向标准正态分布靠拢!从密度函数两侧可以看出t分布的尾部相较标准正态分布的尾部更厚。
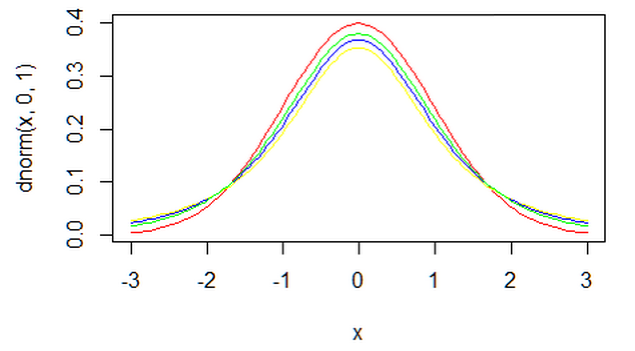
2、从标准正态分布与t分布累积分布函数的比较来看,设P(x)和·Fn(x)分别为标准正态分布和自由度为n的t分布的累积分布函数,当x<0时,有Fn(x)>P(x),当x=0时,有Fn(x)=P(x),当x>0时,有Fn(x)
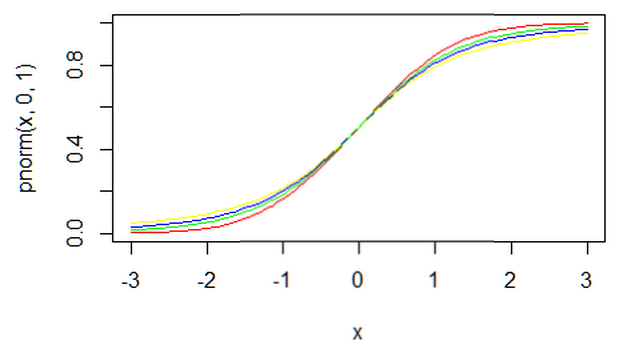
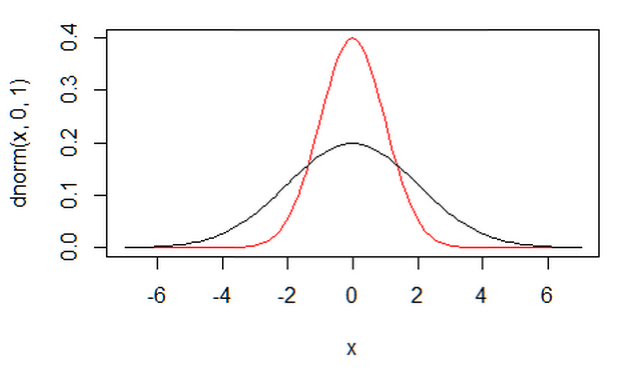
3、从正态分布和t分布的参数来比较,正态分布有两个参数,分别是位置参数mu(正态分布的均值)和形状参数delta(正态分布的方差),delta越大则正态分布密度函数越宽,delta越小则正态分布密度函数越窄。N(0,1)(红色)N(0,2)(黑色)图像如下。而t分布只有一个参数,也就是t分布的自由度,t分布关于x=0对称,自由度的改变只改变t分布密度函数的形状大小,而不改变其位置。
6. 结论及建议
平均使用寿命95%的置信区间,也详细分析了两种型号步枪子弹的枪口速度均值差的一个置信水平位95%的置信区间,通过t分布进行区间估计在实际中的重要应用,体现了t分布的重要作用。
在假设检验中,通过在单样本t检验,判断了元件的平均寿命时常是否大于某一定值,新旧农药在效果上的差异是否显著以及判断了铝材的长度是否满足设定要求.也通过两样本t检验在农业、工业和啤酒业中都得到了应用.在应用分析中,对一些应用借用了SPSS软件进行了分析,得出同样的结论。
t检验的SPSS实现不仅能提高对t检验方法的使用技巧,而且能加深了对统计软件的使用和掌握,从而提高实践技能。
该贴被huang.wang编辑于2018-8-31 11:46:02


 技术讨论
技术讨论