本文转自公众号 算数学苑
在讲隐马尔可夫模型前,先介绍一下什么是马尔可夫链。
马尔可夫链(Markov chain),又称离散时间马尔可夫链,因俄国数学家安德烈·马尔可夫得名,为状态空间中经过从一个状态到另一个状态转换的随机过程。该过程要求具备“无记忆”的性质:下一状态 St +1 的概率分布只能由当前状态 St 决定,与之前的状态无关。
即:
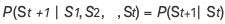
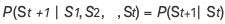
这种特定类型的“无记忆性”称作马尔可夫性质。符合该性质的随机过程则称为马尔可夫过程,也称为马尔可夫链。
马尔可夫过程——“程序猿心情状态”案例
假设有一只程序猿,它每天心情状态有三种:心情舒畅 、心情一般
、心情一般 、心情糟糕
、心情糟糕 。状态间的转移是存在某个概率的。如下图所示:
。状态间的转移是存在某个概率的。如下图所示:
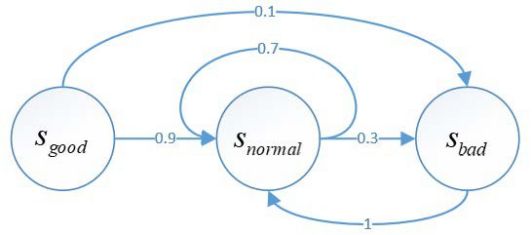
图 1 程序猿心情状态图
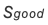 代表心情舒畅状态、
代表心情舒畅状态、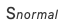 代表心情一般状态、
代表心情一般状态、 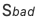 代表心情糟糕状态。
代表心情糟糕状态。
上图表示从当前状态 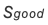 转移到下一时刻状态
转移到下一时刻状态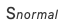 的概率为 0.9,当前状态
的概率为 0.9,当前状态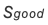 转移到下一时刻状态
转移到下一时刻状态 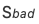 的概率为0.1,当前状态
的概率为0.1,当前状态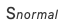 转移到下一时刻还是自身的概率为0.7,当前状态
转移到下一时刻还是自身的概率为0.7,当前状态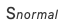 转移到下一时刻状态
转移到下一时刻状态 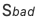 的概率为 0.3,当前状态
的概率为 0.3,当前状态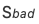 转移到下一时刻状态
转移到下一时刻状态 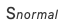 的概率为 1。
的概率为 1。
即为:
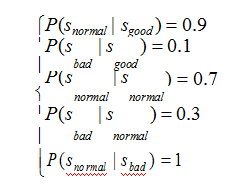
一个含有 N 个状态的马尔可夫链有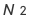 个状态转移。这所有的
个状态转移。这所有的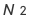 个概率可以用一个状态转移矩阵 A 来表示:
个概率可以用一个状态转移矩阵 A 来表示:

这个状态转移矩阵 A 表示,如果在t 时刻该程序猿的心情状态是舒畅,则在 t+1 时刻的心情状态是舒畅、一般、糟糕的概率分别为(0,0.9,0.1)。
隐马尔可夫模型
隐马尔可夫模型(Hidden Markov Models,简称 HMM)的出现,是为了弥补马尔可夫模型的不足,在某些较为复杂的随机过程中,任一时刻 t 的状态 St 是不可见的。所以观察者没法观察到状态序列 S1 ,S2, L , St ,但是隐马尔可夫模型在每个时刻 t 会输出一个观测状态Ot ,而且Ot 仅和 St 相关。这个被称为独立输出假设。由此可生成一个观测序列O1 , O2 , L , Ot 。
独立输出假设可记为:
P(Ot | O1, O2 ,L, Ot -1, S1, S2 ,L, St ) = P(Ot | St )
隐马尔可夫模型的结构如下:
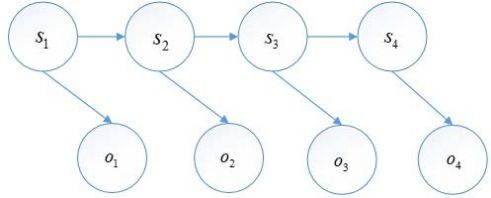
图 2 隐马尔可夫模型结构图
隐马尔可夫模型是由初始概率分布、状态转移概率分布以及观测概率分布确定。隐马尔可夫模型的形式定义如下:
设 Q 是所有可能的状态的集合,V 是所有可能的观测的集合。记为:
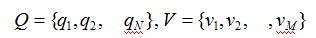
S 是长度为T 的状态序列,O 是对应的观测序列。记为:
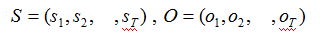
A 是状态转移概率矩阵:
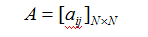
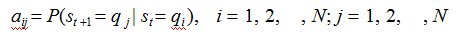
是在时刻t 处于状态qi 的条件下,在时刻 t+1 转移到状态qj 的概率。
B 是观测概率矩阵:
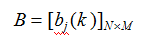
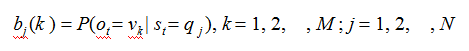
是在时刻t 处于状态qj的条件下,生成观测值Vk的概率。
π是初始状态概率向量:
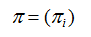
其中,
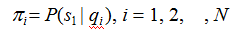
是时刻 t=1 处于状态qj的概率。
隐马尔可夫模型由初始状态概率向量π、状态转移概率矩阵 A 和观测概率矩阵 B 决定。π和 A 决定了状态序列,B 决定观测序列。因此,隐马尔可夫模型λ可以用三元符号表示,即:
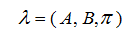
围绕着隐马尔可夫模型通常有 3 个基本问题需要解决:
1、模型评估问题(概率计算问题)
给定模型参数,计算某一观测序列输出的概率。
2、解码问题(预测问题)
给定模型参数和某一观测序列,计算得到最有可能输出这一观测序列的状态序列。
3、参数估计问题(属于非监督学习算法)
给定足够的观测序列集,如何计算得到模型的所有参数。
讲到这,隐马尔可夫模型的理论定义和三个问题都介绍完毕。
可能有朋友会问,这个模型到底有什么用?
先假设我们已经解决了以上的 3 个问题,接下来请看一下典型的通信系统是什么样子的, 想必“隐马尔可夫模型有什么用”这个问题便不攻自破了。
典型的通信系统(该案例参考自吴军《数学之美》第二版,P51)
首先,发送者(人或者机器)发送信息时,需要采用一种能在媒体中(比如空气、电线) 传播的信号,比如语音或者电话线的调制信号,这个过程就是广义上的编码。
然后,通过媒体传播到接收方,这个过程是信道传输。
在接收方,接收者(人或者机器)根据事先约定好的方法,将这些信号还原成发送者的信息,这个过程是广义上的解码。
下图表示了一个典型的通信系统。

图 3 通信模型
其中 S1 , S2 , , Sn 表示信息源发出的信号,比如手机发送的信号。O1 , O2 , Om 是接收器(比如另一部手机)接收到的信号。通信中的解码就是根据接收到的信号O1 , O2 ,LOm ,还原出发送的信号 S1 , S2 ,L, Sn 。
这跟自然语言处理又有什么关系?不妨换个角度来考虑这个问题,所谓的语音识别,就是听者(机器)去猜测说话者要表达的意思。这就像通信系统中,接收端根据收到的信号去还原出发送端发出的信号。
在通信中,如何根据接收端的观测信号O1 , O2 , Om 来推测信号源发送的信息 S1 , S2 , L , Sn 呢?只需要从所有的源信息中找到最可能产生出观测信号的那一个信息。即:
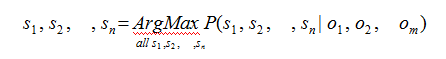
这个公式的意思是,找到一个信息 S1 , S2 , , Sn ,可以使得 P(S1 , S2 , , Sn | O1 , O2 , Om ) 达到最大值。
这个问题其实就是隐马尔可夫模型所提出的第 2 个问题,即解码问题:给定模型参数和某一观测序列,计算得到最有可能输出这一观测序列的状态序列。
接下来我们逐一解决以上 3 个问题,为了计算方便,上述的“程序猿心情状态案例”进行了简化,并修改成了符合隐马尔可夫模型的案例。
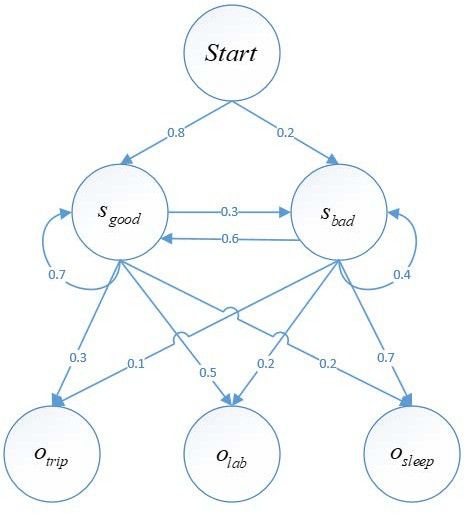
图 4 隐马尔可夫模型“程序猿心情状态”案例升级版
问题求解
在该模型中,初始状态概率向量p = {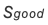 = 0.8,
= 0.8, 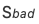 = 0.2},隐藏状态 N=2,可观测状态 M=3,状态转移概率矩阵 A 和观测概率矩阵 B 分别为:
= 0.2},隐藏状态 N=2,可观测状态 M=3,状态转移概率矩阵 A 和观测概率矩阵 B 分别为:
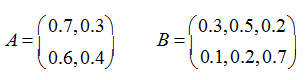
在状态转移概率矩阵 A 中,第 1 行代表t 时刻心情舒畅状态,t+1 时刻心情状态分别是舒畅、糟糕的概率为(0.7,0.3)。第 2 行同理。
在观测概率矩阵B 中,第 1 行代表 t 时刻心情为舒畅状态,t 时刻观测到的程序猿行为状态分别为出门旅游、在实验室写代码、回寝室睡觉的概率分别为(0.3,0.5,0.2)。第 2 行同理。
现在开始解决上述的 3 个问题。
1、模型评估问题(概率计算问题)
模型的各个参数现在已全部知道,假设连续 3 天该程序猿的行为分别是出门旅游→在实验写代码→回寝室睡觉,计算产生这些行为的概率是多少?
解:
求解该问题可以使用遍历法,即把所有可能的情况都计算出来,然后将概率相加。在该
案例中共有 3 种可观测状态,2 种隐藏状态,所以共有23 = 8 种可能的情况。由于该算法较为笨拙且计算繁琐,在此我就计算第一种情况,后面同理可得。其中一种:
第 1 天心情舒畅→第 1 天出门旅游→第 2 天心情舒畅→第 2 天在实验室写代码→第 3 天心情舒畅→第 3 天回寝室睡觉。用符号表达即:
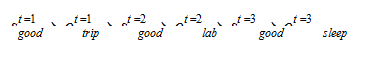
计算过程如下:
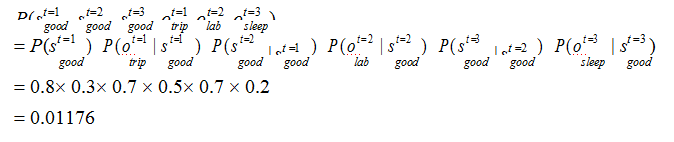
通常求解该问题,使用前向或后向算法,这样计算复杂度会比遍历法有所降低。以前向算法为例求解:
t=1 时,发生 trip 这一行为的概率为:
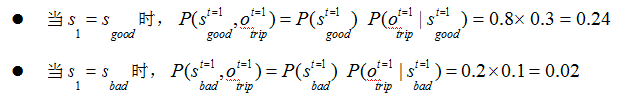
t=2 时,根据上述的独立输出假设,发生 lab 这一行为的概率为:
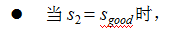
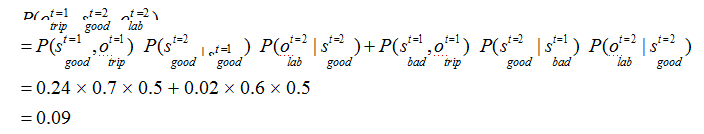
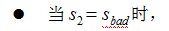
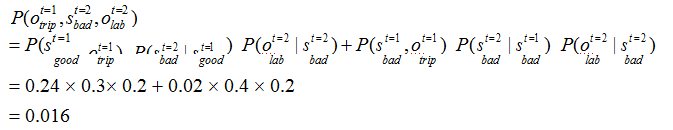
t=3 时,根据上述的独立输出假设,发生sleep 这一行为的概率为:
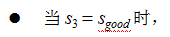
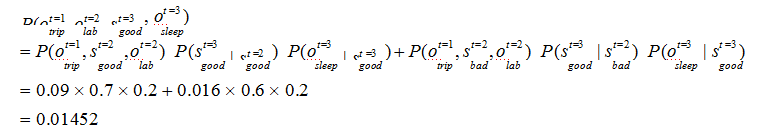
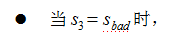
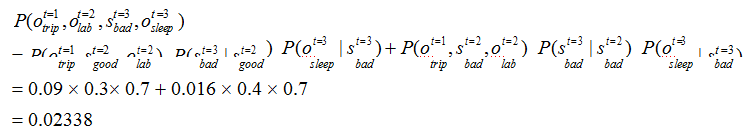
综上,
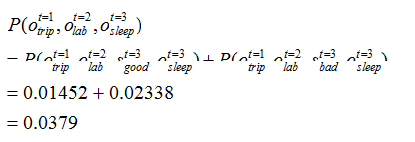
2、解码问题(预测问题)
解决该类问题,通常使用维特比算法。维特比算法是一种动态规划算法,它用于寻找最有可能产生观测序列的隐藏状态序列。

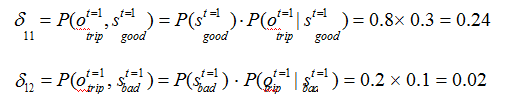

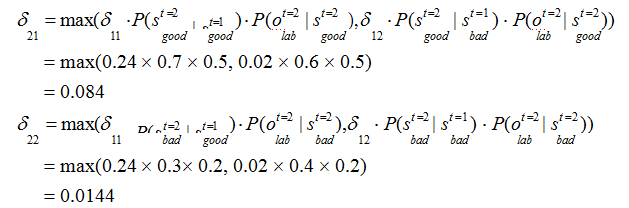
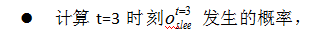
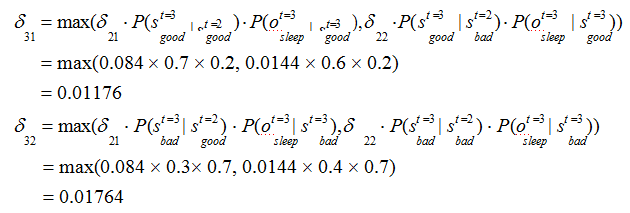
回溯每一步的最大概率:
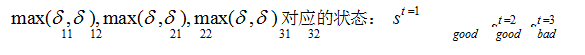
3、参数估计问题(属于非监督学习算法) 参数估计时,有两种不同的估计情况。
第一种是,我们已知大量的隐藏状态集和观测状态集,并且知道它们之间的对应关系, 这样在训练参数时,直接计算各个参数的相对频度即可代替概率。这种情况的数据属于人工标记数据,成本较高,现实中没有这么多的人力和物力去一一标注数据之间的对应关系。
第二种是,我们仅仅可得大量的观测状态集,不知隐藏状态集以及它们之间的对应关系。仅仅通过大量的观测状态集去推测各个参数的方法,称为无监督的训练方法,其中主要使用的是鲍姆-韦尔奇算法。
鲍姆-韦尔奇算法的思想是这样的——首先初始化各个参数的值,值的大小不重要,重要的是要保证这些参数在模型中时,可以输出观测序列。有了初始化的各个参数后,隐马尔可夫模型就算初步齐全了,这时使用该模型输出所有可能的观测序列以及产生这些观测序列的概率。有了这些初步得到的观测序列和概率后,其实就相当于有了一定的人工标注数据,此时再去计算模型的参数, 一步步迭代,直到模型收敛到一个局部最优点。
该贴被huang.wang编辑于2018-8-6 18:08:24


 技术讨论
技术讨论