本文转自公众号 AI科技大本营

引子

最近开始拾起来看一些 NLP 相关的东西，特别是深度学习在 NLP 上的应用，发现采样方法在很多模型中应用得很多，因为训练的时候如果预测目标是一个词，直接的 softmax 计算量会根据单词数量的增长而增长。恰好想到最开始深度学习在 DBN 的时候采样也发挥了关键的作用，而自己对采样相关的方法了解不算太多，所以去学习记录一下，经典的统计的方法确实巧妙，看起来非常有收获。

本篇文章先主要介绍一下经典的采样方法如 Inverse Sampling、Rejective Sampling 以及 Importance Sampling 和它在 NLP 上的应用，后面还会有一篇来尝试介绍 MCMC 这一组狂炫酷拽的算法。才疏学浅，行文若有误望指正。

▌Why Sampling

采样是生活和机器学习算法中都会经常用到的技术，一般来说采样的目的是评估一个函数在某个分布上的期望值，也就是 

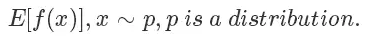
比如我们都学过的抛硬币，期望它的结果是符合一个伯努利分布的，定义正面的概率为 p ,反面概率为 1-p 。最简单地使 f(x)=x，在现实中我们就会通过不断地进行抛硬币这个动作，来评估这个概率p。 

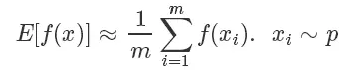
这个方法也叫做蒙特卡洛法（Monte Carlo Method），常用于计算一些非常复杂无法直接求解的函数期望。 

对于抛硬币这个例子来说: 

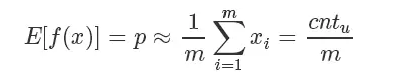
其期望就是抛到正面的计数 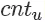除以总次数 m。 

而我们抛硬币的这个过程其实就是采样，如果要用程序模拟上面这个过程也很简单，因为伯努利分布的样本很容易生成： 

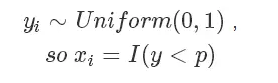
而在计算机中的随机函数一般就是生成 0 到 1 的均匀分布随机数。

▌Sampling Method

可以看到蒙特卡洛法其实就是按一定的概率分布中获取大量样本，用于计算函数在样本的概率分布上的期望。其中最关键的一个步骤就是如何按照指定的概率分布 p 进行样本采样，抛硬币这个 case 里伯努利分布是一个离散的概率分布，它的概率分布一般用概率质量函数（pmf）表示，相对来说比较简单，而对于连续概率分布我们需要考虑它的概率密度函数（pdf）： 

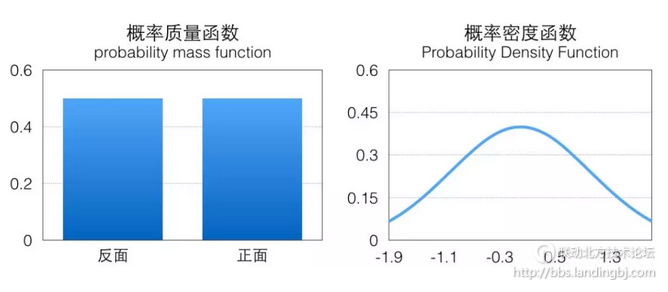
比如上图示例分别是标准正态分布概率密度函数，它们的面积都是 1（这是概率的定义），如果我们可以按照相应概率分布生成很多样本，那这些样本绘制出来的直方图应该跟概率密度函数是一致的。 

而在实际的问题中，p 的概率密度函数可能会比较复杂，我们由浅入深，看看如何采样方法如何获得服从指定概率分布的样本。

▌ Inverse Sampling

对于一些特殊的概率分布函数，比如指数分布： 

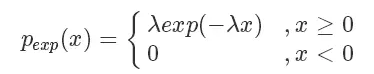
我们可以定义它的概率累积函数(Cumulative distribution function)，也就是(ps.这个’F’和前面的’f’函数并没有关系) 

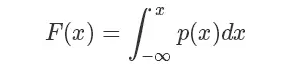
从图像上看就是概率密度函数小于 x 部分的面积。这个函数在 x≥0 的部分是一个单调递增的函数(在定义域上单调非减)，定义域和值域是[0,+∞)→[0,1)，画出来大概是这样子的一个函数，在 p(x) 大的地方它增长快（梯度大），反之亦然：

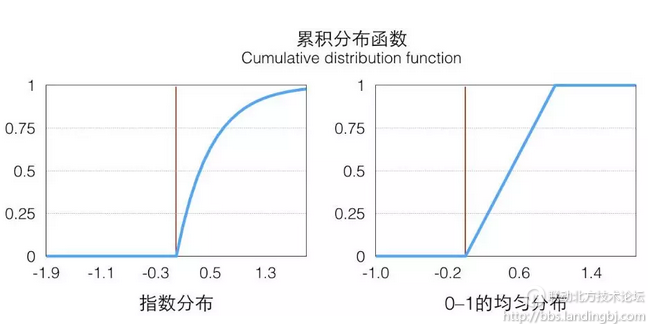
因为它是唯一映射的（在>0的部分，接下来我们只考虑这一部分），所以它的反函数可以表示为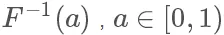 ，值域为[0,+∞)

因为F单调递增，所以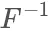也是单调递增的：

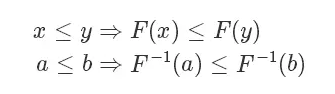
利用反函数的定义，我们有：

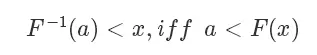
我们定义一下 [0,1] 均匀分布的 CDF,这个很好理解： 

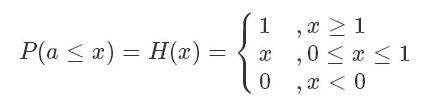
所以 

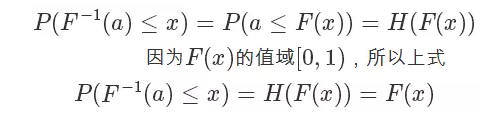
根据 F(x) 的定义，它是 exp 分布的概率累积函数，所以上面这个公式的意思是 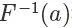 符合 exp 分布，我们通过 F 的反函数将一个 0 到 1 均匀分布的随机数转换成了符合 exp 分布的随机数，注意，以上推导对于 cdf 可逆的分布都是一样的，对于 exp 来说，它的反函数的形式是： 

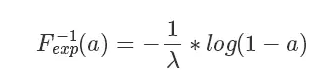
具体的映射关系可以看下图(a)，我们从 y 轴 0-1 的均匀分布样本（绿色）映射得到了服从指数分布的样本（红色）。 

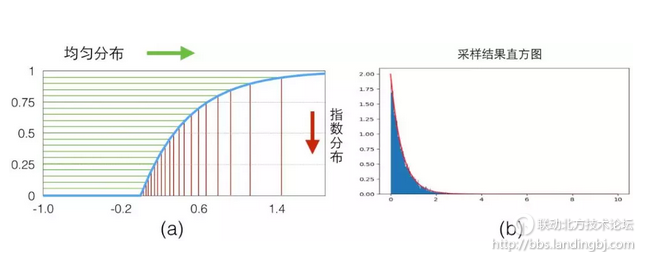
我们写一点代码来看看效果,最后绘制出来的直方图可以看出来就是 exp 分布的图，见上图(b)，可以看到随着采样数量的变多，概率直方图和真实的 CDF 就越接近：

def sampleExp(Lambda = 2,maxCnt = 50000):
    ys = []
    standardXaxis = []
    standardExp = []
    for i in range(maxCnt):
        u = np.random.random()
        y = -1/Lambda*np.log(1-u) #F-1(X)
        ys.append(y)
    for i in range(1000):
        t = Lambda * np.exp(-Lambda*i/100)
        standardXaxis.append(i/100)
        standardExp.append(t)
    plt.plot(standardXaxis,standardExp,'r')
    plt.hist(ys,1000,normed=True)
    plt.show()

▌ Rejective Sampling

我们在学习随机模拟的时候通常会讲到用采样的方法来计算 π 值，也就是在一个 1×1 的范围内随机采样一个点，如果它到原点的距离小于 1,则说明它在1/4 圆内，则接受它，最后通过接受的占比来计算 1/4 圆形的面积，从而根据公式反算出预估的ππ值，随着采样点的增多，最后的结果 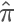 会越精准。 

上面这个例子里说明一个问题，我们想求一个空间里均匀分布的集合面积，可以尝试在更大范围内按照均匀分布随机采样，如果采样点在集合中，则接受，否则拒绝。最后的接受概率就是集合在‘更大范围’的面积占比。

当我们重新回过头来看想要 sample 出来的样本服从某一个分布 p，其实就是希望样本在其概率密度函数 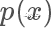 高的地方出现得更多，所以一个直觉的想法，我们从均匀分布随机生成一个样本 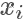，按照一个正比于  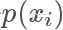的概率接受这个样本，也就是说虽然是从均匀分布随机采样，但留下的样本更有可能是  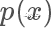高的样本。

这样的思路很自然，但是否是对的呢。其实这就是 Rejective Sampling 的基本思想，我们先看一个很 intuitive 的图

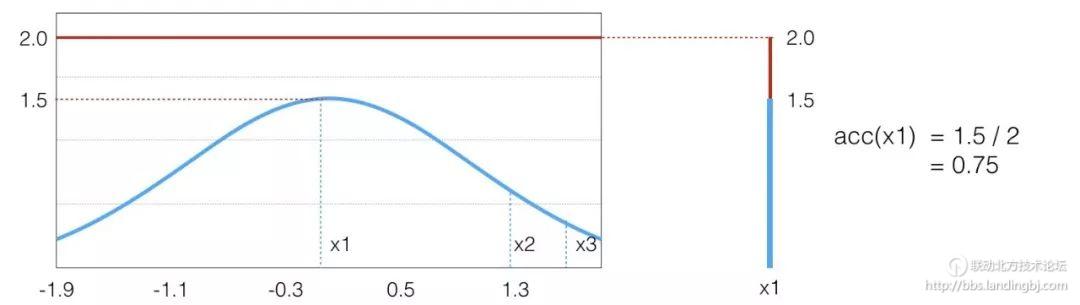
假设目标分布的 pdf 最高点是 1.5,有三个点它们的 pdf 值分别是 

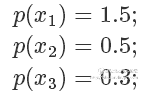
因为我们从 x 轴上是按均匀分布随机采样的，所以采样到三个点的概率都一样，也就是 

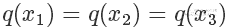
接下来需要决定每个点的接受概率 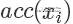，它应该正比于 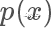，当然因为是概率值也需要小于等于 1. 

我们可以画一根 y=2 的直线，因为整个概率密度函数都在这根直线下，我们设定 

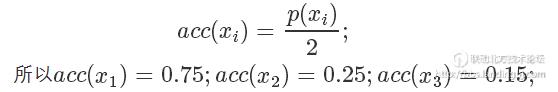
我们要做的就是生成一个 0-1的随机数 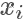，如果它小于接受概率 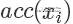，则留下这个样本。因为 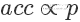，所以可以看到因为  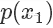是 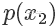 的3倍，所以 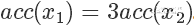。同样采集 100 次，最后留下来的样本数期望也是 3 倍。这根本就是概率分布的定义!

我们将这个过程更加形式化一点，我们我们又需要采样的概率密度函数

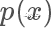，但实际情况我们很有可能只能计算出 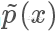,有

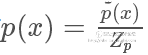
我们需要找一个可以很方便进行采样的分布函数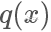并使 

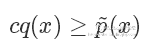
其中 c 是需要选择的一个常数。然后我们从 q 分布中随机采样一个样本 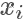,并以 

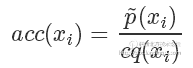
的概率决定是否接受这个样本。重复这个过程就是「拒绝采样」算法了。

在上面的例子我们选择的 q 分布是均匀分布，所以从图像上看其 pdf 是直线，但实际上 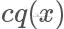 和 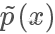 越接近，采样效率越高，因为其接受概率也越高： 

▌ Importance Sampling

上面描述了两种从另一个分布获取指定分布的采样样本的算法，对于1.在实际工作中，一般来说我们需要 sample 的分布都及其复杂，不太可能求解出它的反函数，但 p(x) 的值也许还是可以计算的。对于2.找到一个合适的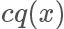往往很困难，接受概率有可能会很低。 

那我们回过头来看我们sample的目的：其实是想求得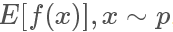，也就是 

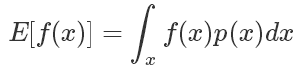
如果符合 p(x) 分布的样本不太好生成，我们可以引入另一个分布 q(x)，可以很方便地生成样本。使得 

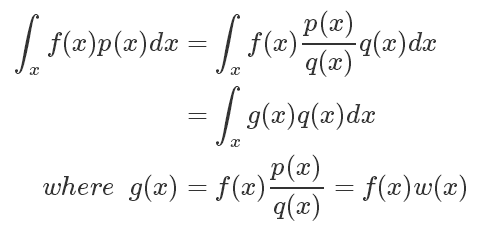
我们将问题转化为了求 g(x) 在 q(x) 分布下的期望！！！ 

我们称其中的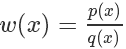叫做 Importance Weight.

▌ Importance Sample 解决的问题

首先当然是我们本来没办法 sample from p，这个是我们看到的，IS 将之转化为了从 q 分布进行采样；同时 IS 有时候还可以改进原来的 sample，比如说: 

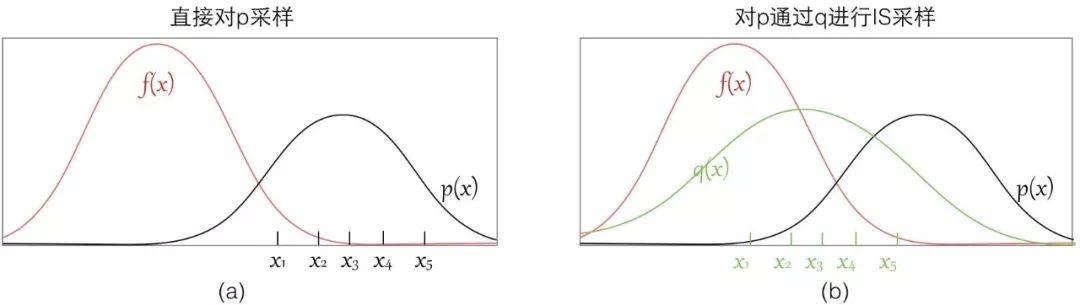
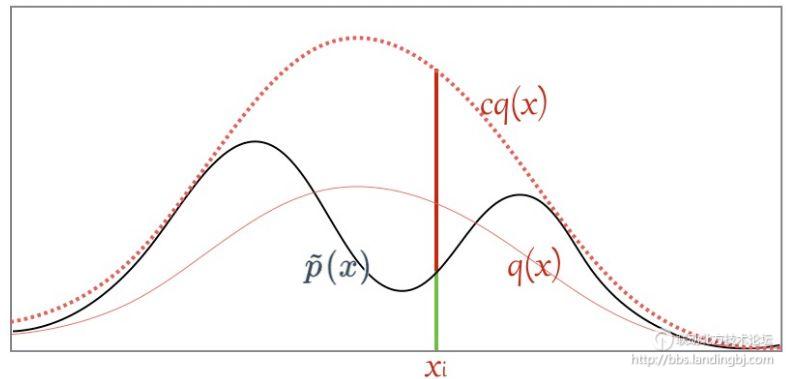
可以看到如果我们直接从 p 进行采样，而实际上这些样本对应的 f(x) 都很小，采样数量有限的情况下很有可能都无法获得 f(x) 值较大的样本，这样评估出来的期望偏差会较大；

而如果我们找到一个 q 分布，使得它能在 f(x)*p(x) 较大的地方采集到样本，则能更好地逼近 [Ef(x)]，因为有 Importance Weight 控制其比重，所以也不会导致结果出现过大偏差。

所以选择一个好的p也能帮助你sample出来的效率更高，要使得 f(x)p(x)较大的地方能被 sample出来。

▌ 无法直接求得p(x)的情况

上面我们假设 g(x) 和 q(x) 都可以比较方便地计算，但有些时候我们这个其实是很困难的，更常见的情况市我们能够比较方便地计算 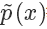 和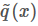 

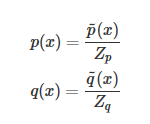
其中 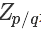 是一个标准化项（常数），使得  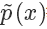或者 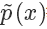 等比例变化为一个概率分布，你可以理解为 softmax 里面那个除数。也就是说

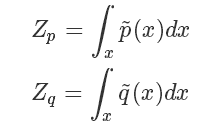
这种情况下我们的 importance sampling 是否还能应用呢？ 

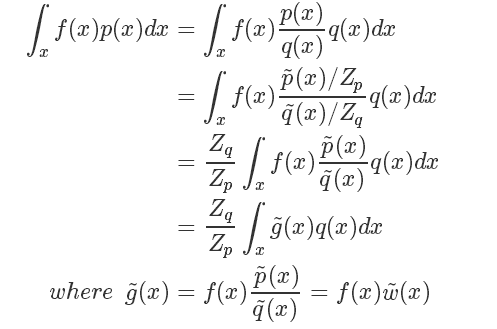
而 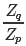 我们直接计算并不太好计算，而它的倒数： 

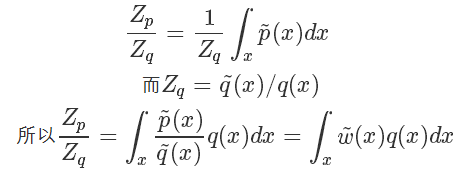
因为我们家设能很方便地从 q 采样，所以上式其实又被转化成了一个蒙特卡洛可解的问题，也就是 

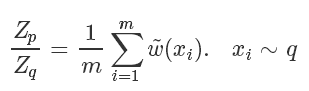
最终最终，原来的蒙特卡洛问题变成了： 

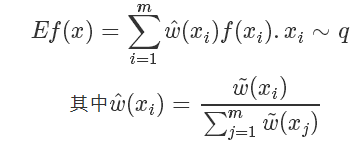
所以我们完全不用知道 q(x) 确切的计算值，就可以近似地从中得到在 q 分布下 f(x) 的取值！！amazing！

▌ Importance Sampling在深度学习里面的应用

在深度学习特别是NLP的Language Model中，训练的时候最后一层往往会使用 softmax 函数并计算相应的梯度。 

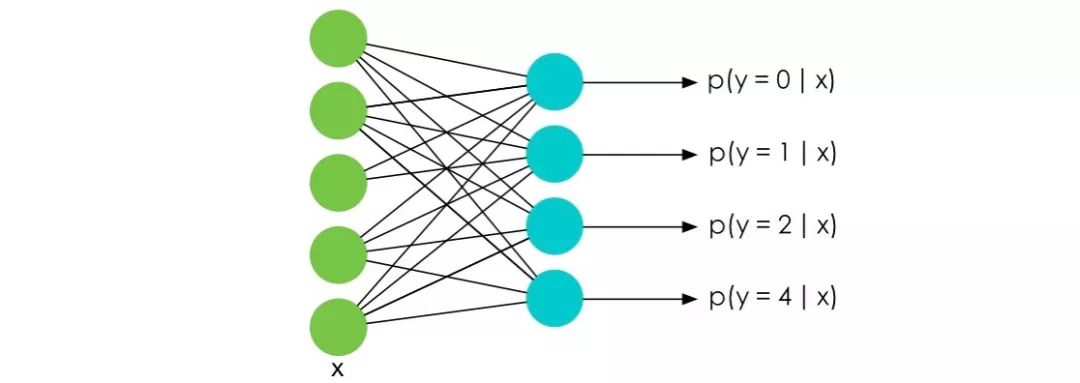
而我们知道 softmax 函数的表达式是： 

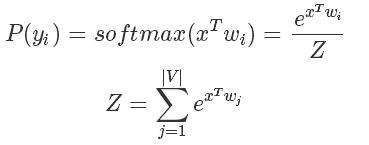
要知道在 LM 中 m 的大小是词汇的数量决定的，在一些巨大的模型里可能有几十万个词，也就意味着计算Z的代价十分巨大。

而我们在训练的时候无非是想对 softmax 的结果进行求导，也就是说 

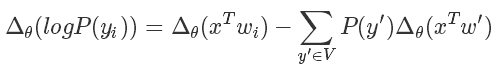
后面那一块，我们好像看到了熟悉的东西，没错这个形式就是为采样量身定做似的。 

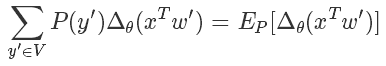
经典的蒙特卡洛方法就可以派上用途了，与其枚举所有的词，我们只需要从 V 里 sample 出一些样本词，就可以近似地逼近结果了。

同时直接从 P 中 sample 也不可取的，而且计算 P是非常耗时的事情（因为需要计算Z），我们一般只能计算 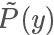，而且直接从 P 中 sample 也不可取，所以我们选择另一个分布 Q 进行 Importance Sample 即可。

一般来说可能选择的 Q 分布是简单一些的 n-gramn 模型。下面是论文中的算法伪代码，基本上是比较标准的流程（论文图片的符号和上面的描述稍有出入，理解一下过程即可）： 

References

【1】mathematicalmonk’s machine learning course on y2b. machine learing 

【2】Pattern Recognition And Machine Learning 

【3】Adaptive Importance Sampling to Accelerate Training of a Neural Probabilistic Language Model.Yoshua Bengio and Jean-Sébastien Senécal