本文转自 玄数的博客

公元 1777 年的一天，法国科学家布丰的家里宾客满堂，原来他们是应主人的邀请前来观看一次奇特试验的。

试验开始，但见年已古稀的布丰先生兴致勃勃地拿出一张纸来，纸上预先画好了一条条等距离的平行线。接着他又抓出一大把原先准备好的小针，这些小针的长度都是平行线间距离的一半。然后布丰先生宣布：“请诸位把这些小针一根一根往纸上扔吧！不过，请大家务必把扔下的针是否与纸上的平行线相交告诉我。”

客人们不知布丰先生要干什么，只好客随主意，一个个加入了试验的行列。一把小针扔完了，把它捡起来又扔。而布丰先生本人则不停地在一旁数着、记着，如此这般地忙碌了将近一个钟头。最后，布丰先生高声宣布：“先生们，我这里记录了诸位刚才的投针结果，共投针 2212 次，其中与平行线相交的有 704 次。总数 2212 与相交数 704 的比值为 3.142。”说到这里，布丰先生故意停了停，并对大家报以神秘的一笑，接着有意提高声调说：“先生们，这就是圆周率π的近似值！”

π在这种纷纭杂乱的场合出现，实在是出乎人们的意料，然而它却是千真万确的事实。由于投针试验的问题，是布丰先生最先提出的，所以数学史上就称它为布丰问题。布丰得出的一般结果是：如果纸上两平行线间相距为d，小针长为 l，投针的次数为 n，所投的针当中与平行线相交的次数是 m，那么当 n 相当大时有：π≈2ln/dm

上面故事中，针长l恰等于平行线间距离d的一半，所以代入上面公式化简得：π≈n/m

其中的一个证明方法是：找一根铁丝弯成一个圆圈，使其直径恰恰等于平行线间的距离 d。可以想象得到，对于这样的圆圈来说，不管怎么扔下，都将和平行线有两个交点。因此，如果圆圈扔下的次数为 n 次，那么相交的交点总数必为 2n

现在设想把圆圈拉直，变成一条长为πd 的铁丝。显然，这样的铁丝扔下时与平行线相交的情形要比圆圈复杂些，可能有 4 个交点，3 个交点，2个交点，1 个交点，甚至于都不相交。

由于圆圈和直线的长度同为πd，根据机会均等的原理，当它们投掷次数较多，且相等时，两者与平行线组交点的总数可望是一样的。这就是说，当长为πd 的铁丝扔下 n 次时，与平行线相交的交点总数应大致为 2n。

现在再来讨论铁丝长为 l 的情形。当投掷次数 n 增大的时候，这种铁丝跟平行线相交的交点总数 m 应当与长度 l 成正比，因而有：m＝kl，式中 K 是比例系数。为了求出 K 来，只需注意到，对于 l＝πd 的特殊情形，有 m＝2n。于是求得k=2n/πd。代入前式就有m≈2ln/πd，从而π≈2ln/dm

这便是著名的布丰公式。

但这个证明有个问题，就是证明的基础：当铁丝的长度一定时，无论什么形状，与线相交，为什么点的总数期望是一样的呢？为什么它们是机会均等的？

我所重新研究的布丰投针试验

布丰投针试验是一个著名求π值的试验，然而其背后的原因却鲜有人知晓。今天我们就要让布丰实验中针线相交的概率不再只是一个数字，而是一场刺激的数学竞斗。

如下所示，布丰投针试验的过程十分简单，就是在一张理想的，画满无数条等距平行线的纸上随机投下一根根细针，让针自由倒下，之后统计针和平行线相交的频率，当投针次数越来越多时，将此频率取倒数，就可以得到一个有趣的数值。

在平行线间距为针长两倍时，这个数值为π，也就是我们最熟知的版本。

现在，我们将分析更为普遍的情况下，布丰投针试验中针线相交的概率，并以此探明它和圆周率π之间神秘莫测的关系。为了方便起见，我们按照布丰投针试验的初步逻辑，假设针长为l，平行线间距为a。

在整个实验过程中，因为平行线是无限的，所以对于每一根针，无论最后针落在哪里，在倒下之前都必定落在两相邻平行线间，当它倒下以后，若相交也只会与这两条线中的一条相交，否则就不与平行线相交，因此我们就可以把问题简化为研究两条相邻平行线间的针线相交问题，这样的简化可以囊括一切针线相交时的情形，它并不会改变我们所求的概率，却可以使我们面临的复杂问题变得一目了然。

在本次实验中，我们不讨论横向距离。因为平行线无限长，所以对于针的初始落点，只有其纵向距离有讨论价值，而横向距离并无影响。

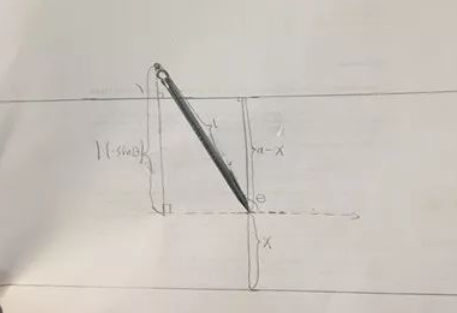
当我们了解了上述内容后，我们令针随意落在一点，与两平行线中更低的一条的距离为X，之后随机倒向一角度θ，为方便讨论，我们以平行线右向为极轴，令针的角度θ在-π与π之间。我们对之前的实验结果进行分析，此时针线相交的情况便可以归纳为以下两者之一。

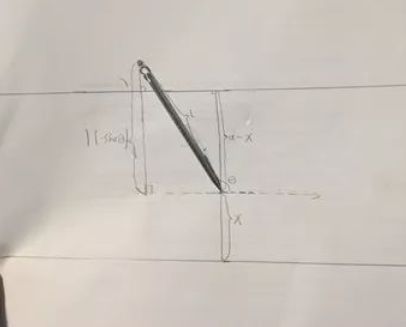
①当情况如上图所示（我们的实验结论），也就是θ在0与π之间（针向“上”倒）时，如果此时落点太往下，使a-x大于l*|sinθ|了，针就没有办法和更高的线相交了，而如果要使针和更低的线相交，如下图所示，我们就需要把落点不断下移才行。

可是别忘了此时的情况是针往上倒，所以说如果落点要满足大假设，落在两平行线间，那只有a-x=0才有可能，但是很明显如此具体的落法的概率是零。因此若要相交，则必有0小于等于a-X小于等于l*lsinθl，也就是a-l.sinθl 小于等于X小于等于a。

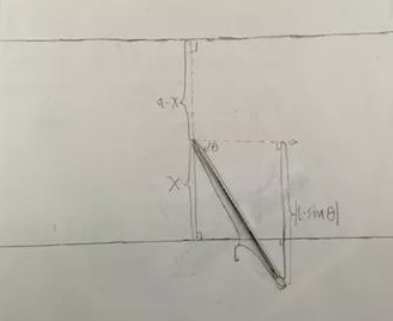
②当情况如上图所示，也就是θ在-π与0之间（针向“下”倒）时，可知此时如果落点太往上了，与之前相似，它无法和更低的线相交，而如果要和更高的线相交，如下图所示，我们就要不断把落点上移。

但是同样的，此时落点位于顶部平行线的上方，这是不满足大假设的。所以如果要满足大假设，则a-x必须等于0，这也是零概率的。故同理，此时有X小于等于l*lsinθl,又因为X大于等于0才能满足大假设，故此时有0小于等于X小于等于l*lsinθl。

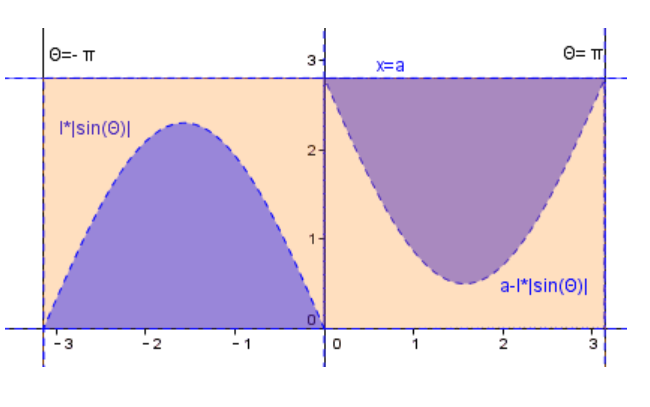
此时，作θ-X图像（如上图），我们把x与θ的所有可能取值绘出以后可以得到浅橙色的矩形，而如果我们把之前的使针线相交的不等式也在坐标系中绘出，我们可以得到蓝色的阴影部分，可知蓝色阴影部分为使针与线相交的所有（θ，X）值。而浅橙色部分为所有可能的（θ，X）值。

那么，当我们有了这些以后，我们如何计算概率呢？我们知道在讨论从表示全体可能值的面积中取出某一部分的概率，可以通过这一部分的面积和表示全体可能值的面积比得到，即：P=S阴/S全。

又因为S阴等于

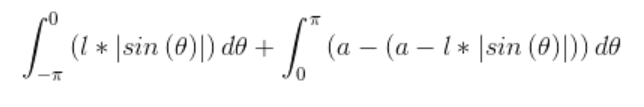
也等于

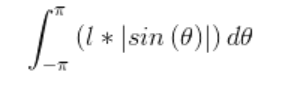
将绝对值符号打开以后，利用牛顿-莱布尼茨定理则不难发现，积分值为l*(cos(0)-cos(-π)+(-cos(π))-(-cos(0)))=l*(1-(-1)+(-(-1))-(-1))=l*(1+1+1+1)=4*l，而s全=2π*a，因此p=4l/(2πa)=2l/(aπ)，我们就得到了布丰投针试验的理想概率。

扩展

既然我们做出了这样的结论，那么它是否适用于一切l和a呢？答案是否定的，因为一旦我们取一根特别长的针，使l大于a，比如说l=100a，此时如果我们贸然使用结论，将会得到概率为200/π，约为6366.2%，这很明显是不可能的，那么究竟是哪里出了错呢？如下图所示，应该是我们用来表示满足条件的(x,θ)区域的面积，也就是积分本身出现了谬误。

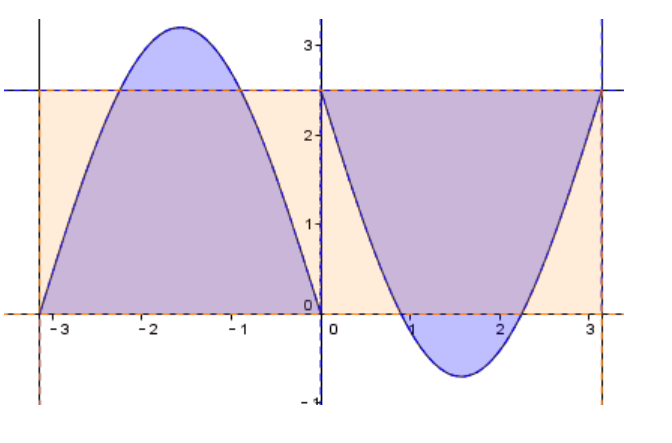
原来是因为l大于等于a时，我们最开始使用的积分表示的的阴影部分有一部分超出有效界限了，故积分已不能正确表达使针线可相交的合理（θ，X）区域，正确形状应如下图所示。

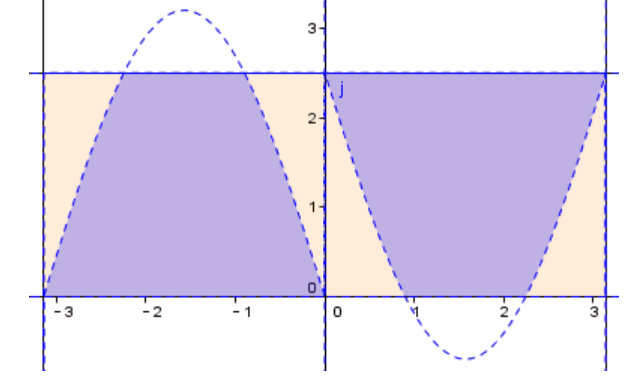
此时的蓝色阴影部分面积才是正确的满足条件的（θ，X）区域，那么我们如何构造积分来计算这个面积呢，我们不难发现，两块形状其实是一模一样的，因此我们只需要通过积分求出其中一块的面积，另一块的面积也自然迎刃而解。为了方便起见，我们讨论左边的面积。

很明显它其实是一个分段函数，在-π到l*lsinθl=a的较小解和l*lsinθl=a的较大解到0这两个区间上，它等于l*|sinθ|，但在两个解之间的区间上，它则单纯等于a，从而我们需要先求出l*lsinθl=a在-π与0之间的两个解，才好继续处理问题。利用反三角函数，结合两解均在-π与0之间的直观条件，我们可以得到较小解应该是arcsin(a/l)-π，而较大解则是-arcsin(a/l)。

因此，去绝对值后，我们的积分就是-l*sinθ在-π到arcsin(a/l)-π上的积分，加上a在arcsin(a/l)-π到-arcsin(a/l)上的积分，再加上-l*sinθ在-arcsin(a/l)到0上的积分，算出来以后就是左边的阴影部分面积了。继续应用牛顿-莱布尼茨定理，可以得到值应该为

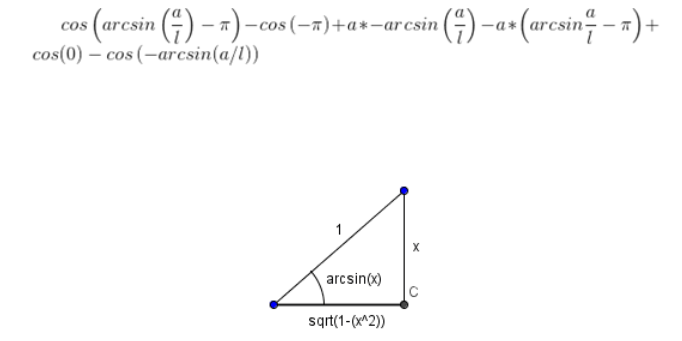
利用几何法（结合上图），不难得到cos(arcsin(x))=sqrt(1-x^2)，将x代入我们的情况（令x=a/l），也就可以得到其反正弦函数的余弦为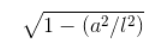，结合三角函数的性质（例如cos(-x)=cos(x)，cos(π-x)=-cos(x)之类的），我们不难发现，所求的积分值化简后即为

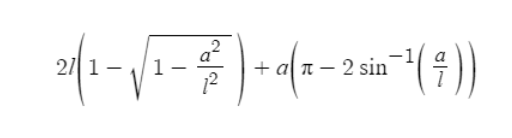
将它乘以2（表示左边面积与右边面积之和）后除以2a*π，即可得到正确的概率p。

此时，p=

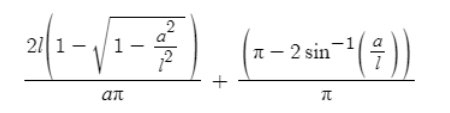
比较它与l小于a时的形式，我们可以发现这两项在l小于a时均没有意义，前者因为那时会使根号下出现负数，而后者则因为反正弦函数的定义域不能超过1，同时我们可以发现第一项即为l小于a时的概率乘以(1-aqrt(1-a^2/l^2)，这是由于区域中这部分面积仍与l*|sin(θ)|有关所造成的。如果我们研究l=a时的临界情况，我们会发现此时第二项为0，而第一项则刚好仍等于2l/(aπ)，因此这两个表达式之间的过渡也是我们所知的了。

关于布丰投针试验，我们还可以进行一些有趣的改动，例如周期性改变平行线间距，或者改变投下物体的形状等，但是最后的相交概率，仍可以用本浅析的思想进行解决！